線形写像が単射、全射になる必要十分条件

動機
#

よく使うのでまとめた。

写像ってなんすか？
#

って方向けに簡単に写像のイメージを説明しておく。

さっさと本題を見たい方は目次から飛んでください。

中学生の頃にwikipediaを漁っていたら写像に関しての記述を見つけて、おなじみの図が載せられていたが当時はなんのことだが全くわからなかった。

写像という文字を見るとかなり手強そうに見えるが、要は2つの集合の要素と要素の対応のことだ。

では集合とは何かというと、簡単に言ってしまえばモノや概念の集まりだ。

テーブルの上に乗っているコインの集まりも集合だし、部屋にあるダンボールの中に入っているみかんの集まりも集合と言える。

スケールを大きくして、地球上に存在する全ての18歳の女性という集合を考えることができる。

そして、集合の要素とは、最後の例で言えば、隣りにいる僕の彼女(18歳)や隣の部屋に住んでいるあの子(18歳)などの文字通りに集合を構成する要素の事だ。

もちろん数学的な概念の集合も考えることができる。
10以上100未満の整数の集合を考えることもできるし、自然数全体、実数全体の集合を考えることもできる。

要素が無限にある集合は無限集合と呼ばれる。

要素が一つもない集合は空集合($\emptyset$)と呼ばれる。

これらの説明は厳密ではないのでイメージ程度でとどめておいてください。

単射(injection)とは
#

単射とは、集合$X, Z$に関する写像$f: X \to Z$が$X$の異なる元(要素) $$ x,\space y　(x \neq y) $$

に対して常に

$$ f(x) \neq f(y) $$ を満たすことをいう。

つまり、定義域の、異なる要素$x, y$の行き先$f(x), f(y)$がダブらないということだ。

俺もそんな椅子取りゲームのない優しい世界に生まれたかったよ。

左側の楕円は集合X、右側の楕円は集合Zを表している。
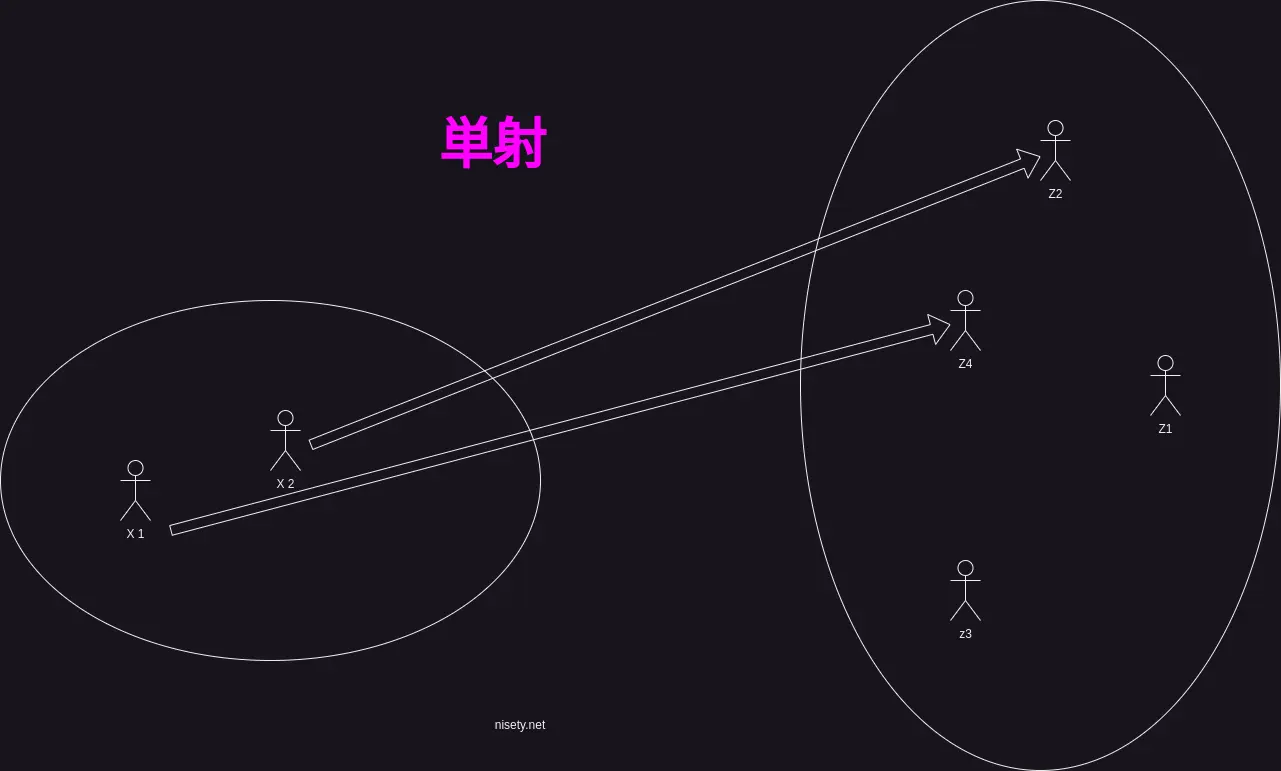
楕円内の人型はそれぞれの集合の要素を表している。

全射(surjection)とは
#

全射とは、集合$X, Z$に関する写像$f: X \to Z$が

$$ \forall z \in Z,\space \exists x \in X ,\space f(x) = z $$ を満たすことをいう。

日本語で言うと、全ての$Z$の要素$z$に対して、$f(x) = z$を満たすような$x$と$f$が必ず存在するということだ。

上の2つの表現は回りくどいので、もっと分かりやすく言うと、fの行き先がZを埋め尽くすということだ。

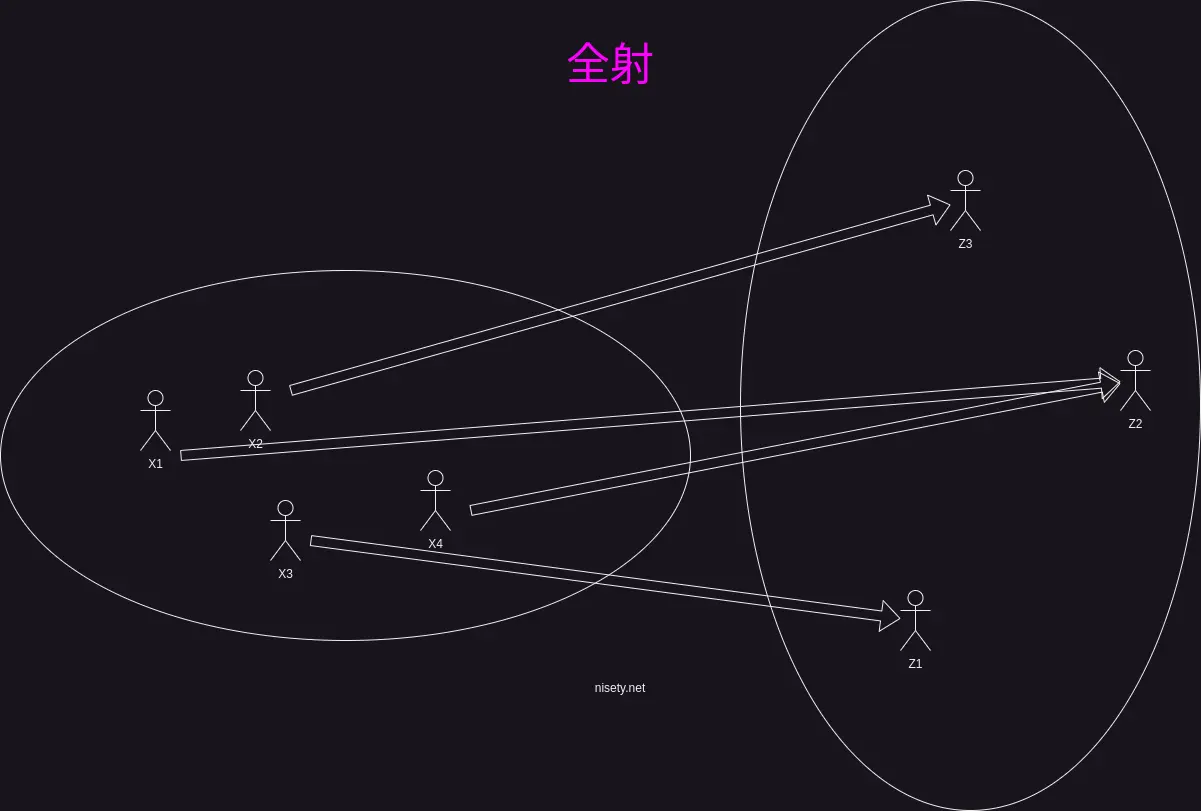
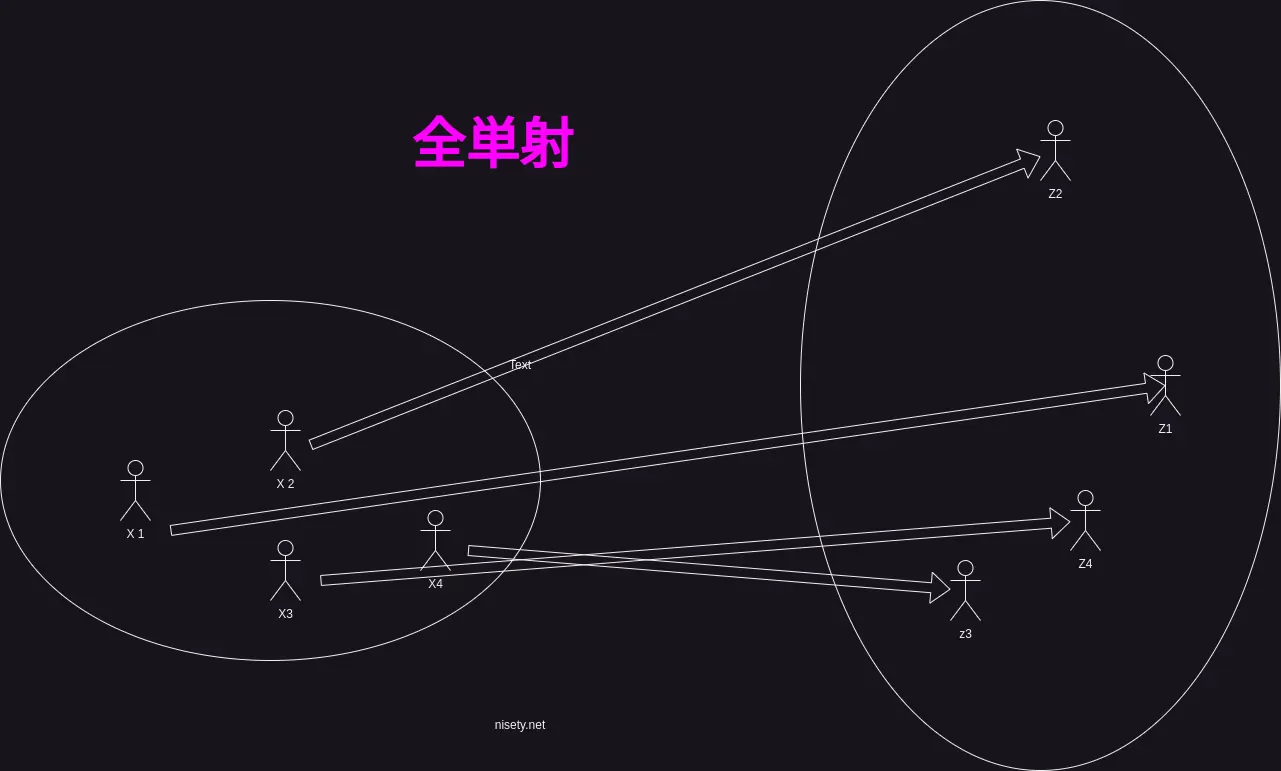
全単射(bijection)とは
#

単射かつ全射。

線形写像が単射、全射、全単射であるための必要十分条件
#

ここからが本題だ。
drawioという、図を書けるツールを試してみたかったので試しに上に基本的な説明を書いてみた。
良い感じだ。

$V, W$をベクトル空間、$f$を$f: V \to W$の線形写像とする。

単射
#

$$ Ker f=\lbrace \bm{0} \rbrace $$ つまり、 $$ \dim Im f = \dim V $$

証明
#

補足。線形写像はゼロベクトルをゼロベクトルへ写す。

線形写像の定義より、$f(k\bm{v})=kf(\bm{v})$なので、
$$ f(\bm{0})=f(0\bm{0})=0f(\bm{0})=\bm{0} $$

$Ker f=\lbrace \bm{0} \rbrace \implies f$が単射
#

$Ker f=\lbrace \bm{0} \rbrace$であると仮定する。

いま、$V$のベクトル$\bm{v_1}, \bm{v_2}$が$f(\bm{v_1}) = f(\bm{v_2})$を満たしたとする。

$$ f(\bm{v_1}) = f(\bm{v_2}) \\ f(\bm{v_1}) - f(\bm{v_2}) = \bm{0} \\ f(\bm{v_1} - \bm{v_2}) = \bm{0} \space \because fの線形性 $$ となる。
よって、$\bm{v_1}-\bm{v_2} \in Ker f$なので、$\bm{v_1}-\bm{v_2} = \bm{0} \implies \bm{v_1} = \bm{v_2} $

つまり$f$は単射。

$f$が単射 $\implies Ker f=\lbrace \bm{0} \rbrace$
#

$f$が単射だと仮定する。

$V$の$\bm{0}$以外の任意のベクトル$\bm{v}$に対して、$f$は単射なので、
$$ f(\bm{v}) \neq f(0) = 0 $$ つまり、行き先が$W$の$\bm{0}$になるような$V$のベクトルは$\bm{0}$しかないので$Ker f=\lbrace \bm{0} \rbrace$となる。