球体で自作ゲームの衝突検出を実装する

サムネイルは自作ゲームと関係ありません。

衝突検出とは
#

ゲームや物理シミュレーションなどのソフトウェアでは、プレイヤーや敵、物体、飛沫などを頂点の集合のオブジェクト(モデル)で表現する。
その上にテクスチャを貼り付けたり、光の反射具合などを調整して見た目をつくる。

ほとんどの3Dゲームではプレイヤーは地面に立つ必要があるし、壁にぶつかれば衝突を検出して止まったりする必要がある。

物理シミュレーションでも、物体同士がぶつかったら速度や質量などのパラメーターに応じて跳ね返りの挙動を再現する必要がある。

ある物体と別の物体が衝突しているか検出することを衝突検出と言う。そのまんまだ。

GPUとディスプレイはあくまでDirectXやVulkan、OpenGLなどを通して頂点やテクスチャを指示されたとおりに処理して表示するだけなので、そういった処理は自分で書かないといけない。

俺達に残された選択肢
#

自分が実装している自作ゲームは、所謂UnityやUnrealEngine、Godotなどのゲームエンジンを利用していない。

wgpuというDirectXやVulkan、OpenGLなどのバックエンドの差異が吸収されたライブラリ(?)を利用して描画している。

プレイヤー目線からすればクソシンプルな割に、コードはめちゃくちゃゴチャってるold schoolなコンピューターゲームだ。

自分のその環境では大まかに分けて2つの選択肢があった。
他者が作成した既存の衝突検出ライブラリを利用するか、自分で衝突検出ライブラリを実装するかだ。

ただゲームを完成させるだけなら前者で良い。
そもそもゲームエンジンを使わずにwgpuを直接扱おうと思ったのは、どのように図形や物体を描画するのか、カメラはどのように実装すればよいのかなどを主に知りたかったからだ。

衝突検出を少しでも知っておきたいと思ったので前者は最終手段にすることにした。

しかし、それなりに機能の揃った衝突検出ライブラリを自作するのは、リサーチしてすぐに簡単な事ではないことが分かった。

よって、間を取って、機能の限定された衝突検出を自前で実装することにした。

自分のゲームはシンプルなので単純な衝突検出で事足りる。
おそらくライブラリ化(共通化)するまでもないレベル。

具体的にどうやって衝突検出するか
#

先程、ゲームやシミュレーションの衝突検出の話をしたが、具体的にどのように衝突を検出するのか、軽く調べた結果をまとめておく。

ゲーム上の物体、例えば人形キャラクターなどは、多くの頂点から構成されており(🔗小さな三角形をつなげて複雑なオブジェクトを表現するのが一般的)、形状も複雑でそのまま衝突検出するには計算的なコストが高すぎる。

シミュレーションは場合によるが、ゲームの場合はフレームレートを維持しなければならないので、60fpsのゲームでは1fに約16.7ms(約0.0167秒)しか計算する時間が与えられない。

16.7msの中でゲームのロジックの実行や状態の更新、衝突検出を行わないといけないのであまり時間はかけられない。

そこで、複雑なモデルで衝突検出する代わりに、モデルに似た単純な図形で衝突を検出することによって衝突検出のコストを下げるテクニックが用いられる。

単純な図形にはAABB(Axis-aligned Bounding Boxes)と呼ばれる直方体や球、🔗凸包(convex hull)などが利用される。

どれを使うかだが、状況によって要請は異なるので一般的な最適解があるわけではない。

ゲームをやっている人は当たり判定、喰らい判定、判定といった言葉を知っている人が多いだろう。

格闘ゲームやモンスターハンターの当たり判定もこのBV(Bounding Volume)という単純な図形で実装されていることが多い。(はず。)

クリックで拡大

長方形でキャラクターの当たり判定、技の攻撃判定が実装されている。
このゲームは2Dだが、単純な図形を利用するという基本は同じ。
ゲーム名は🔗あすか120％スペシャルVer.2。

BVで交差していたら更に詳細な衝突検出をするなんてこともできる。

BVを利用しても、BVの数が多すぎると愚直に衝突検出した場合、計算コストが大きくなるので工夫する必要がある。

愚直にn個のオブジェクトの衝突検出をしようとすると、n個のオブジェクトの中から重複なしで2個選ぶ組み合わせになるのでnC2通り計算しなければならない。

${}_2 \mathrm{C} {}_2 = 1 $
${}_4 \mathrm{C} {}_2 = 6 $
${}_{10} \mathrm{C} {}_2 = 45 $
${}_{50} \mathrm{C} {}_2 = 1225 $
${}_{100} \mathrm{C} {}_2 = 4950 $
${}_{500} \mathrm{C} {}_2 = 124750 $
${}_{1000} \mathrm{C} {}_2 = 499500 $
${}_{4500} \mathrm{C} {}_2 = 10122750 $

といった感じだ。

最初のうちならともかく4500とかになるともう明らかに無理だろう。

計算量を減らすために、オブジェクトを大まかにグループ分けする。(n-body processing)

そして、後に各々のグループ内で個別に(BVを利用したりして)衝突検出を行う。(pair processing)

わかりやすく言うと、十分に離れている物体と物体はまず衝突しないのでその衝突検出の処理を飛ばそうという試みだ。

コンピューターが目で見て自動で十分離れているか人間のように判断してくれるわけではないので、空間をうまく距離の近い物体の集まりで分割するアルゴリズムが必要となる。

具体的な説明は省くが、それがうまく機能したらどのくらい負荷が改善されるのか計算してみる。

500個のオブジェクトが運良く10つのグループに別れたとすると、
$$ {}_{50} \mathrm{C} {}_2 $$ が10つなので、

$$ {}_{50} \mathrm{C} {}_2 \cdot 10 = 12250 $$ となり、

$ {}_{500} \mathrm{C} {}_2 = 124750 $なので細かい衝突検出の数はこの例では約1/10に改善されることになる。

衝突検出の触りを調べた結果をまとめたが、これだけでも面倒なことが伝わっただろう。

自作ゲームで簡易的な衝突検出を実装する
#

自分が作ろうとしているゲームでは、衝突検出の必要な物体は立方体で、動きもマスに合わせたものと3方向の回転のみなので、楽をできるはず。

AABB、球が要請を満たすのでどちらが良いか実装を比較してみる。

AABB
#

AABBの交差判定はx, y, z方向の全ての辺が重なっていれば交差しているとわかる。

2Dで考えると分かりやすい。

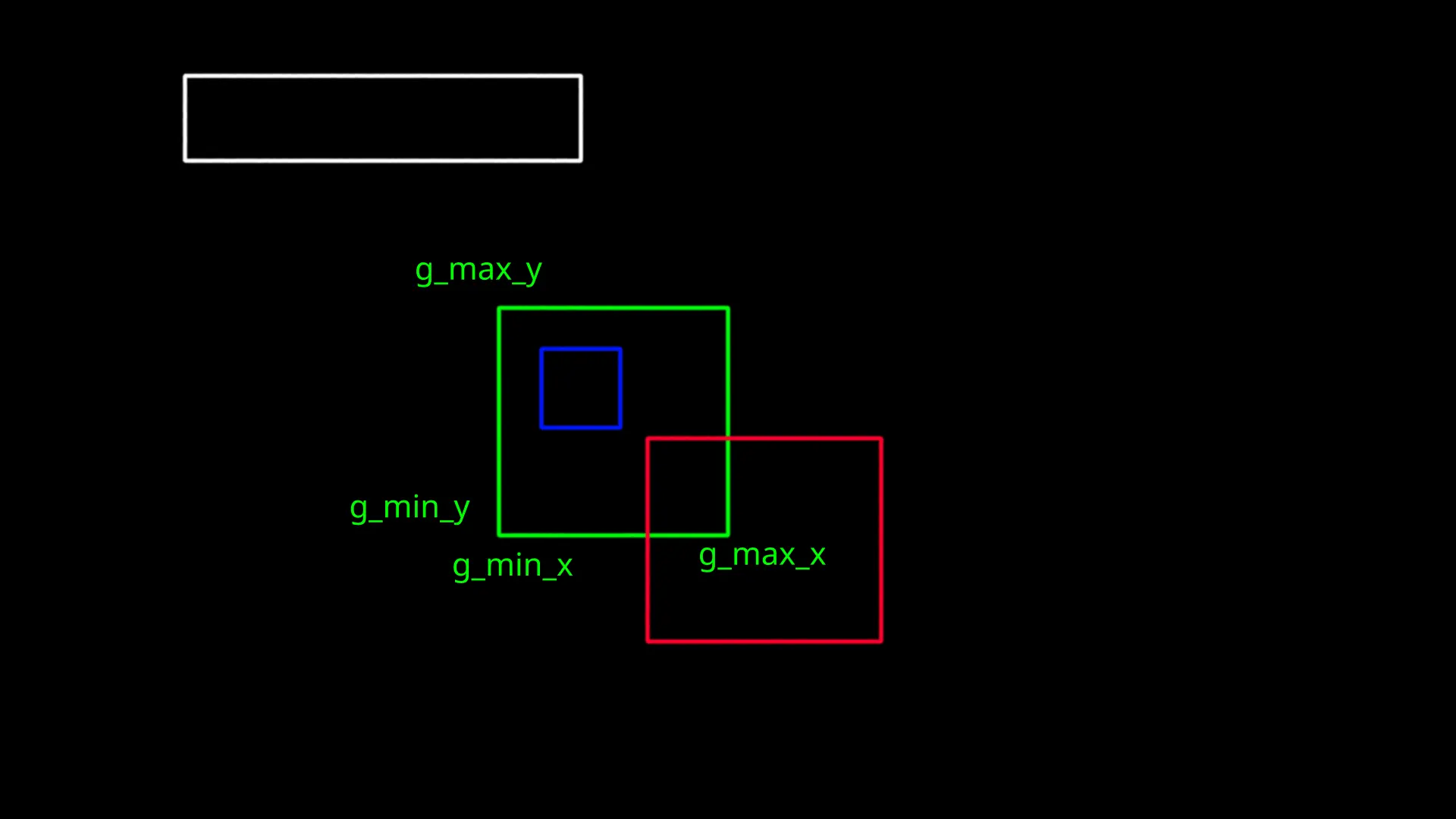
いま、平面上に4つの長方形が存在する。

g_min_xは緑色(Green)の長方形の左端のX座標。
g_max_xは緑色(Green)の長方形の右端のX座標。
g_min_yは緑色(Green)の長方形の下端のY座標。
g_max_yは緑色(Green)の長方形の上端のY座標。

AABB(Axis-aligned Bounding Boxes)なので、座標軸に対して斜めになっている長方形は考えなくて良い。
斜めだと話が変わってくる。

実装ではうまく衝突検出したい対象の物体の形を囲むような斜めになっていない長方形、直方体を生成しなければならない。

重なっている状態を直接判定しようとすると、例外パターンなどがあって面倒なので重ならない条件でふるいにかけて該当しなければ重なっていると判定する。

物体が2つあれば、それらは重なっているか重なっていないかのどちらかなので(少なくとも今、自分たちが考えている空間においては)、この手法が使える。
🔗排中律ってヤツだ。

そのことを踏まえて上の画像を観察すると、以下のようなコードで交差を検出することができることが分かる。


struct Vector2{
    float x;
    float y;
};

struct Box{
    Vector2 min;
    Vector2 max;
};

// 2つのBox(長方形)の構造体を受け取って交差しているかどうか判定する関数
bool is_intersecting(Box const & box1, Box const & box2){
    // 一方の長方形の左端が、片方の長方形の右端より大きければ絶対に交差しない。
    if (box1.max.x < box2.min.x){ return false ;}
    if (box2.max.x < box1.min.x){ return false ;}

    //　ここに到達すれば、少なくとも片方の軸で交差

    // 一方の長方形の下端が、片方の長方形の上端より大きければ絶対に交差しない。
    if (box1.max.y < box2.min.y){ return false ;}
    if (box2.max.y < box1.min.y){ return false ;}

    // ここに到達すれば、両軸で交差しているので重なっている。
    return true;
}

3Dの場合、z軸の同様の処理を追加してあげれば良い。

とAABBは比較的簡単に交差テストできることが分かったが、衝突検出対象のオブジェクトがAxis-aligendでない半端な回転などをした場合が面倒なので、回転に強くて単純な別のBVを探すことにする。

円、球
#

それは何かというと、2Dでは円で、3Dでは球だ。

円の線は平面上である一点から、ある一定の距離に存在する点の集合で構成される。
球はその3D版だ。

ある一定の距離とは半径のことだ。

平面上の円を考えて感覚を掴んでおく。

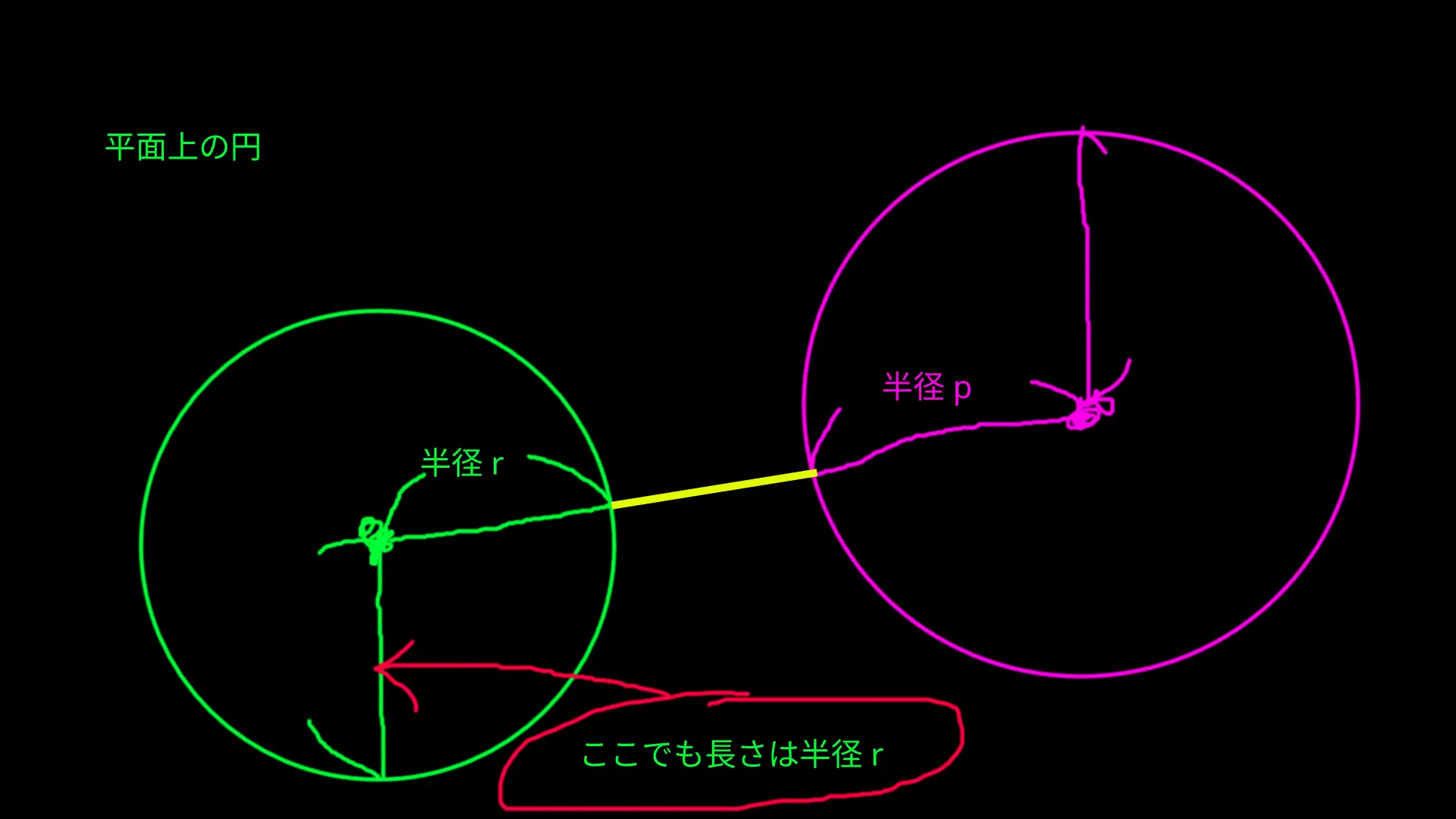
緑の円は半径r、ピンクの円は半径pだ。
円の中心から円の線に真っ直ぐな線を引けばどれも長さが半径に等しくなる。

半径rと半径pと黄色の線が一直線上に並んでいるところに注目してほしい。
2つの円が交差していないことは明らかだろう。
なぜなら、黄色の線分の距離があるからだ。
そして、これが円、球体の交差判定の原理だ。

球や円はその定義上、回転しても何も影響がないのも強みとなる。
救世主だ。

と、やることは分かったので球の交差判定がどのような感じになるかC++の疑似コードで実装してみる。

struct Vector3{
    float x;
    float y;
    float z;
};

struct Sphere{
    Vector3 pos; // 球の中心点の座標
    float radius; // 半径
};

bool is_intersecting(Sphere const & sp1, Sphere const & sp2){
    const Vector3 sub = sp1 - sp2; // Vector3に-演算子が定義されていると仮定。

    // 2つの球の半径の和を計算
    const float radius_sum = sp1.radius + sp2.radius;

    // 距離の2乗を比較
    return (sub.dot(sub) <= radius_sum * radius_sum); // dot(内積)関数が定義されていると仮定。
}

コード内の、subベクトルの長さを求めれば、2つの球の間の距離を求めることができるが、sqrtは計算コストが高いので工夫で避けている。

ベクトル$\bm{v}$の長さとは$\lVert \bm{v} \rVert$のことで、 $$ \lVert \bm{v} \rVert=\sqrt{ (\bm{v},\bm{v}) } $$ だった。$(\bm{v},\bm{v})$は🔗ベクトルの内積。

内積の成分表示についてはこちら: 🔗ベクトルの内積　成分表示での公式の証明

成分で見ると、 $$ \bm{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} \\ \lVert \bm{v} \rVert= \sqrt{ (\bm{v},\bm{v}) } =\sqrt{ x^2 + y^2 + z^2 } $$ で確かに距離が求められている。
🔗平面，空間上の2点間の距離について

ここで、$\lVert \bm{v} \rVert=\sqrt{ (\bm{v},\bm{v}) }$の両辺を2乗すると、 $$ \lVert \bm{v} \rVert^2=(\bm{v},\bm{v}) $$ であることと、$a \leqq b$という大小関係は$a^2 \leqq b^2$としても変わらないことを利用して、

$\lVert \bm{v} \rVert^2$と半径の和radius_sumの2乗を計算して比較することでも目的を達成できることが分かる。

自分の場合は、ゲーム上の制約から球で大まかな判定を表現するだけで事足りたが、球では判定が大雑把すぎるなど(例えば箱を球で囲むとかなり体積に差が出る)、不適切な場合もあるのでその場合はAABBや別の図形の組み合わせを利用するしかない。

幸い、自分のゲームはこれぐらいの簡単な交差テストで衝突検出できるはずなのと、勉強したい事が多くて余力がないのでここまでにしておく。

いつか衝突検出を本格的に学ぼうとする日が来るのだろうか。