同値関係、同値類、商集合、商ベクトル空間(商線形空間)とは？

動機

#

線形変換と不変部分空間あたりを理解しようとして藻掻いていたが、どうやら商ベクトル空間をある程度理解しないといけないようなので。

自分がメインで使っている参考書の商ベクトル空間の記述は同値関係などの前提知識について何も触れられていなかったので、そこらへんも学習ついでにまとめておいた。

事前準備

#

本題に入る前にいくつか必要な前提知識があるので軽くまとめておく。

同値関係(equivalence relation)

#

例えば、適当な自然数\(a, b, c\)に関して、=では、
\(a = a\) 反射律(reflexive)
\(a = b \implies b = a\) 対称律(symmetric)
\(a = b, \space b = c \implies a = c\)　推移律(transitive)
が成り立つ。

この=という関係を拡張、一般化した概念が同値関係だ。
同値関係は二項関係(binary relation)の一種である。

Binary relation: 🔗https://en.wikipedia.org/wiki/Binary_relation

集合\(X\)上の関係\(\sim\)が以下を全て満たすとき、\(\sim\)は集合\(X\)上の同値関係と呼ばれる。
\(x,\space y,\space z \in X\)とする。

1. \(x \sim x\) (反射律)
2. \(x \sim y \implies y \sim x\) (対称律)
3. \(x \sim y, \space y \sim z \implies x \sim z\) (推移律)

\(x \sim y\)のとき、\(x,\space y\)は\(\sim\)によって同値であるという。

先程の=もこの同値関係の一種である。

同値類(equivalence class)

#

集合\(X\)上の同値関係\(\sim\)について、

集合\(X\)の要素、\(x \in X\)に関して、 $$ [x] \coloneqq \lbrace y \in X |\space x \sim y \rbrace $$ で定義される集合\([x]\)を(\(X\)の)\(\sim\)による同値類という。
また、\(x\)を\([x]\)の代表元という。

\([x]\)は日本語で言えば、集合\(X\)のある要素\(x\)に関して、\(x\)と同値関係にある\(X\)の要素全てからなる集合だ。

厳密には同値類はequivalence classという名の通り集合ではなくて類(class)らしいが、classには集合であるsmall classと、集合でないproper classがあり、集合論の外の文脈ではclassは集合として扱われることが多いとのこと。
🔗https://en.wikipedia.org/wiki/Class_(set_theory)

\(x \sim x\)なので、\(x \in [x]\)である。

定義から分かるように、同値類に属する任意の元はその同値類の代表元になることができる。

商集合

#

集合\(X\)とその上の同値関係\(\sim\)について、 $$ X/\sim \space \coloneqq \lbrace [x] |\space x \in X \rbrace $$ で定義される集合\(X/\sim\)を\(X\)の同値関係\(\sim\)による商集合という。
\(X\)の同値類の全体である。

\([x]\)は同値類であり、集合なので、\(X/ \sim\)は集合の集合である。

同値類、商集合の性質

#

集合\(X\)と同値関係\(\sim\)について以下が成り立つ。

同値類の元は同じ同値類をつくる

#

つまり、 \(y \in [x] \implies [y] = [x]\)である。

証明

#

推移律で示される。

\(y \in [x]\)とすると、\(x \sim y\)であり、 $$ [y] = \{ z \in X | \space y \sim z \} \\ = \{ z \in X | \space x \sim z \} = [x] $$

異なる同値類は元を共有しない

#

\([x] \neq [y] \implies [x] \cap [y] = \emptyset \)

証明

#

\([x] \neq [y]\)かつ\([x] \cap [y] \neq \emptyset \)と仮定すると、\(\exists z \in [x] \cap [y]\)であり、同値類の元は同じ同値類をつくることから、\([z] = [x] = [y]\)である。

しかしこれは、\([x] \neq [y]\)に矛盾するので、\([x] \cap [y] = \emptyset\)である。

\(X\)上の各々の同値類の元をすべて集めると全体になる

#

つまり、 $$ \underset{x \in X}{\bigcup} [x] = X $$ である。

一応補足しておくが、\(\underset{x \in X}{\bigcup} [x]\)の意味はXの同値類\([x_1], \space \dots ,\space [x_n]\)に対して、 \([x_1] \cup [x_2] \cup \dots \cup [x_n]\)である。

証明

#

まず、\(\underset{x \in X}{\bigcup} [x] \subset X\)は明らかだろう。

任意の\(a \in X\)について、\(a \in [a]\)かつ\([a] \subset \underset{x \in X}{\bigcup} [x] \)なので、
\(a \in \underset{x \in X}{\bigcup} [x] \)であり、\(X \subset \underset{x \in X}{\bigcup} [x] \)が示される。

よって、\(\underset{x \in X}{\bigcup} [x] = X\)

ベクトル空間上の商集合

#

\(V\)を(体\(K\)上の)ベクトル空間、\(W\)をその部分空間とする。

ベクトル空間に同値関係を導入する

#

\(\bm{a}, \space \bm{b} \in V \)として、\(V\)上の同値関係\(\bm{a} \sim \bm{b}\)を $$ \bm{a} \sim \bm{b} \iff \bm{a} - \bm{b} \in W $$ と定義する。

日本語で言えば、\(V\)のベクトル\(\bm{a},\space \bm{b}\)の差\(\bm{a} - \bm{b}\)の結果が\(W\)の要素であるとき、\(\bm{a} \sim \bm{b}\)とするということだ。

ベクトルの差はベクトル空間の公理にないんじゃないの？　と思った方は以下の記事を読んでみてほしい。
確かに差は直接に要請されていない。
🔗関連記事: 抽象ベクトル空間と部分空間の復習メモ

同値関係を満たしていることを確認する。

反射律

#

\(\bm{a} - \bm{a} = \bm{0}_V = \bm{0}_W \in W\)

\(\bm{0}_V\)は\(V\)のゼロベクトル。
\(\bm{0}_W\)は\(W\)のゼロベクトル。

\(\bm{a} - \bm{a} = \bm{0}_V\)であるのはベクトル空間の公理の加法の逆元の定義より。
ではなぜ\(\bm{0}_V = \bm{0}_W\)なのだろうか？　と思った方は以下の記事内で解説しているのでそちらを確認していただきたい。
🔗関連記事: 抽象ベクトル空間と部分空間の復習メモ

対称律

#

\(\bm{a} \sim \bm{b}\)とすると、\(\bm{a} - \bm{b} \in W \)である。 \(W\)は部分空間なので、ベクトル空間である。

よって、いま、\(\bm{b} - \bm{a}\)を考えると、 $$ \bm{b} - \bm{a} = -(\bm{a} - \bm{b}) \in W $$ である。

\(\bm{a} - \bm{b} \in W\)であれば、ベクトル空間の公理より加法の逆元が存在するから\(-(\bm{a} - \bm{b}) \in W\)となるわけだ。

推移律

#

\(\bm{a} \sim \bm{b}\)、\(\bm{b} \sim \bm{c}\)とする。
\(\bm{a} - \bm{b} \in W\)、\(\bm{b} - \bm{c} \in W\)より、 $$ (\bm{a} - \bm{b}) + (\bm{b} - \bm{c}) = \bm{a} - \bm{c} \in W $$ つまり、\(\bm{a} \sim \bm{c}\)である。

\(\sim\)が確かに\(V\)上の同値関係であることが示された。

ベクトル空間の商集合を定義

#

\(V\)に同値関係を導入できたので、\(V\)に関して、先程述べた商集合を考えることができる。

\(W\)を\(V\)の部分空間として、\(\bm{v} \in V\)に対して、
$$ [\bm{v}] = \lbrace \bm{u} \in V | \space \bm{u} \sim \bm{v} \rbrace = \lbrace \bm{u} \in V | \space \bm{u} - \bm{v} \in W \rbrace \\ V/\sim = \lbrace [\bm{v}]| \space \bm{v} \in V \rbrace $$ とする。
\(V/\sim\)は\(V\)の\(\sim\)による商集合である。

\(\bm{x} - \bm{y} \in W\)と同値な条件

#

\(\bm{x} \in V\)に対して、 $$ \bm{x} + W \coloneqq \{ \bm{x} + \bm{y} | \space \bm{y} \in W \} $$ という記号を導入する。
あるベクトル\(\bm{x}\)に\(W\)の全てのベクトルをそれぞれ足した結果の全体の集合である。
この記事で頻出するので留意を。

以下の2つの条件は同値である。

1. \(\bm{x} - \bm{y} \in W\)
2. \(\bm{x} + W = \bm{y} + W \)

\(2 \implies 1\)の証明

#

\(W\)はベクトル空間なので\(\bm{0}\)を含み、 $$ \bm{x} = \bm{x} + \bm{0} \in \bm{x} + W $$ なので、仮定より\(\bm{x} + W = \bm{y} + W \)であり\(\bm{x}\)は\(\bm{y} + W\)にも含まれることがわかる。

\(\bm{y} + W\)にも含まれるということは、ある\(W\)のベクトル\(\bm{w}\)で\(\bm{x} = \bm{y}+ \bm{w} \)で表されるということである。

したがって、\(\bm{x} - \bm{y} = \bm{w}\)である。

\(1 \implies 2\)の証明

#

\(\bm{x} - \bm{y} =\bm{w}_1\)とすると、仮定より\(\bm{w}_1 \in W\)である。
\(W\)は部分空間なので、任意の\(\bm{w} \in W\)に対して\(\bm{w} + \bm{w}_1 \in W\)である。

いま、\(\bm{z} \in \bm{x} + W\)とすると、ある\(\bm{w} \in W\)で\(\bm{z} = \bm{x} + \bm{w}\)と表せる。

$$ \bm{z} = \bm{x} + \bm{w} = \bm{x} - \bm{w}_1 + \bm{w}_1 + \bm{w}\\ = \bm{x} - (\bm{x} - \bm{y}) + \bm{w}_1 + \bm{w} = \bm{y} + (\bm{w}_1 + \bm{w}) \in \bm{y} + W $$ であるから、\(\bm{x} + W \subset \bm{y} + W\)が成り立つ。

\(\bm{x}, \space \bm{y}\)を入れ替えて同様の議論をすることにより、\(\bm{y} + W \subset \bm{x} + W\)となるので、\(\bm{x} + W = \bm{y} + W\)が成立する。

商ベクトル空間(商線形空間, quotient vector space)

#

先程の議論によって、 $$ [\bm{v}] = \{\bm{u} \in V| \space \bm{u} - \bm{v} \in W \} = \{ \bm{u} \in V| \space \bm{u} \in \bm{v} + W \} = \bm{v} + W $$ となる。

等号成立についての補足(クリックで展開)

2つ目の等号は\(\bm{u} - \bm{v} \in W \)ということは、ある\(\bm{w} \in W\)で、\(\bm{u} - \bm{v} = \bm{w}\)と表されることであり、式変形によって\(\bm{u} = \bm{v} + \bm{w}\)となることより。

上述の同値の議論がどう関係しているかについては、見えにくくなってしまっているが、\(\{\bm{u} \in V| \space \bm{u} - \bm{v} \in W \}\)という集合を別の形で表すのに、 $$ \bm{u} - \bm{v} \in W \iff \bm{u} + W = \bm{v} + W $$ より、\(\bm{u} + W = \bm{v} + W\)なので、\(\{ \bm{u} \in V| \space \bm{u} \in \bm{v} + W \}\)という集合を考えれば、\(\bm{v} + W\)の元であるということは、\(\bm{u} + W\)の元でもあるので、
\(\{ \bm{u} \in V| \space \bm{u} \in \bm{v} + W \}\)と記述すれば、暗に\(\bm{u} + W = \bm{v} + W\)、つまり\(\bm{u} - \bm{v} \in W\)であるベクトル\(\bm{u}\)を全て記述していることになり等号が成立するところに関わっている。

説明が下手くそかな。

3つ目の等号は\(\{ \bm{u} \in V| \space \bm{u} \in \bm{v} + W \}\)について、この集合は\(\bm{u}\)が\(V\)全体を"動いて"構成されるので、\(\bm{v}+W = \{ \bm{u} \in V| \space \bm{u} \in \bm{v} + W \}\)となることより。

この関係によって、\(V/\sim\)を別の形で表現することができる。
$$ V/W \coloneqq V/\sim = \lbrace [\bm{v}]| \space \bm{v} \in V \rbrace = \lbrace \bm{v} + W| \space \bm{v} \in V \rbrace $$

この\(V/W\)に和やスカラー倍を定義したものが商ベクトル空間だ。

\(V/W\)に演算を定義する

#

和とスカラー倍を以下のように定義する。
$$ (\bm{u} + W) + (\bm{v} + W) \coloneqq (\bm{u} + \bm{v} + W) \space ( \bm{u} + W, \space \bm{v} + W \in V/W) \\ \lambda (\bm{u} + W) \coloneqq (\lambda \bm{u}) + W \space (\lambda \in K, \space \bm{u} + W \in V/W) $$

この和とスカラー倍について\(V/W\)はベクトル空間となる。

\(V/W\)の和とスカラー倍がwell-definedであるかどうか確認する

#

同値類に関しての文脈でwell-definedという言葉が使われたときは、代表元の取り方によっておかしなこと(矛盾や不都合、不整合)にならないという意味をもつ。

詳しくは🔗関連記事: 同値類の演算に関して、well-defined, ill-definedとは？に分けて記述したのでそちらを参照していただきたい。

和はwell-defined

#

\([\bm{u}], \space [\bm{v}] \in V/W\)として、 \(\bm{u}_1, \space \bm{u}_2 \in [\bm{u}]\)、 \(\bm{v}_1, \space \bm{v}_2 \in [\bm{v}]\)をそれぞれ\([\bm{u}], \space [\bm{v}]\)の異なる代表元とする。

\([\bm{u}_1] + [\bm{v}_1] =[\bm{u}_2] + [\bm{v}_2] \)が示されれば、和は代表元のとり方に依らないといえる。

$$ [\bm{u}_1] + [\bm{v}_1] = [\bm{u}_1 + \bm{v}_1] \\ = [\bm{u}_1 - \bm{u}_2 + \bm{u}_2 + \bm{v}_1 - \bm{v}_2 + \bm{v}_2] \\ = [\bm{u}_1 - \bm{u}_2] + [\bm{u}_2] + [\bm{v}_1 - \bm{v}_2] + [\bm{v}_2] \\ = [\bm{u}_2] + [\bm{v}_2] $$

最後の変形でなぜ、 \([\bm{u}_1 - \bm{u}_2], \space [\bm{v}_1 - \bm{v}_2]\)が消えるのか一見分かりにくいが、\(\bm{u}_1 \sim \bm{u}_2\)なので、\(\bm{u}_1 - \bm{u}_2 \in W\)であり、[]の定義を確認すると、\([\bm{u}_1 - \bm{u}_2]\)は\(W\)と一致することが分かる。
よって、\([\bm{u}_1 - \bm{u}_2]= (\bm{0} + W)\)となり、和の定義は
$$ (\bm{u} + W) + (\bm{v} + W) \coloneqq (\bm{u} + \bm{v} + W) $$ だったので $$ [\bm{u}_1 - \bm{u}_2] + [\bm{u}_2] =(\bm{0} + W) + (\bm{u}_2 + W) = (\bm{u}_2 + W) $$ となって、なかったことになる。

スカラー倍はwell-defined

#

\([\bm{u}] \in V/W\)として、 \(\bm{u}_1, \space \bm{u}_2 \in [\bm{u}]\)をそれぞれ\([\bm{u}]\)の異なる代表元とする。

\(\lambda [\bm{u}_1] = \lambda [\bm{u}_2]\)であれば、スカラー倍は代表元のとり方に依らないといえる。

$$ \lambda [\bm{u}_1]=[\lambda \bm{u}_1] \\ = [\lambda \bm{u}_1 - \lambda \bm{u}_2 + \lambda \bm{u}_2 ] \\ = [\lambda (\bm{u}_1 - \bm{u}_2)] + \lambda [\bm{u}_2 ] \\ = \lambda [\bm{u}_2 ] $$

\([\lambda (\bm{u}_1 - \bm{u}_2)]\)が消滅する理由は和の方の説明と同様。

\(V/W\)はベクトル空間の公理を本当に満たしているのか確認する

#

ベクトル空間の公理(🔗関連記事: 抽象ベクトル空間と部分空間の復習メモ)を満たすことを確認する。

和に関して閉じている

#

\([\bm{u}], \space [\bm{v}] \in V/W\)とする。

定義より、和は $$ [\bm{u}] + [\bm{v}] = [\bm{u} + \bm{v}] $$ であり、\(\bm{u} + \bm{v} \in V\)なので閉じている。

定義より、\(V/W = V/\sim = \lbrace [\bm{v}]| \space \bm{v} \in V \rbrace \)だったので、[]の中が\(V\)のベクトルであれば閉じていると言える。

スカラー倍に関して閉じている

#

\([\bm{u}] \in V/W, \space \lambda \in K\)とする。

$$ \lambda [\bm{u}]= [\lambda \bm{u}] \in V/W \because \lambda \bm{u} \in V $$

その他の規則、商ベクトル空間のゼロベクトル

#

その他のベクトル空間の公理について、参考書などでは省略されているが、一応、自分が商ベクトル空間に馴染みたかったので示しておくことにした。

と思ったが、手を付けたらどれも捻りなしで示すことができることに気がついたので、やめておくことにした。

強調しておきたいのは、\(V/W\)のゼロベクトルは\([\bm{0}]\)、つまり、\((\bm{0} + W)\)もっと言えば、\(W\)であることだ。
\(\bm{0}\)ではない！！！！
そもそも、\(\bm{0}\)は\(V/W\)の元ですらない！！

これがおかしいと思うのであれば、抽象ベクトル空間を誤って解釈している可能性が高いので、🔗関連記事: 抽象ベクトル空間と部分空間の復習メモ内の抽象ベクトル空間の定義と抽象ベクトル空間の具体例(の注意点の項)を参考にしていただければと思う。

参考までに、挙動は $$ [\bm{0}] + [\bm{u}] = [\bm{0} + \bm{u}] = [\bm{u}] $$ といった感じだ。

商ベクトル空間の具体例

#

抽象的な定義だけでは誤解釈してしまう恐れがあるので、適当な具体例を見ておくことにした。

\(\Reals^3\)の商ベクトル空間の一例

#

\(\Reals ^3\)とその部分空間 $$ W = \{ \begin{pmatrix} x \\ y \\ 0 \end{pmatrix} | x, \space y \in \Reals \} $$ \(\Reals^3\)の話なので、3次元空間上で視覚的にとらえることができる。
\(W\)は\(z=0\)のxy平面になる。

この部分空間\(W\)による商ベクトル空間は $$ \Reals^3 /W = \{ [\bm{v}] | \space \bm{v} \in \Reals^3 \} = \{ \bm{v} + W | \space \bm{v} \in \Reals^3 \} $$ である。

この商空間も\(W\)と同様に視覚的にとらえることができる。

せっかくなので図に表してみよう。

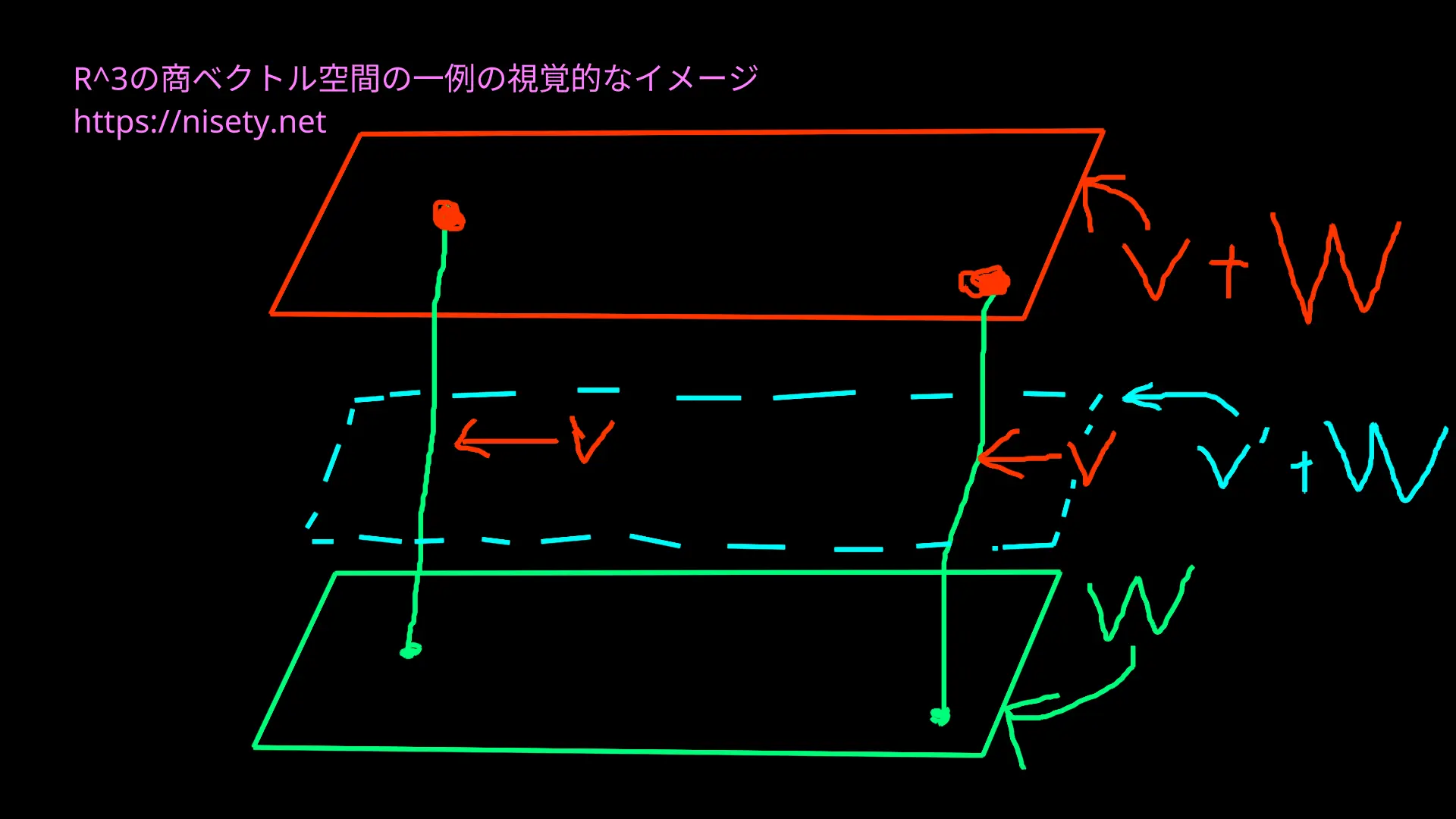
\(\bm{v} + W\)という演算で平面\(W\)がベクトル\(\bm{v}\)で平行移動されていることが分かるだろう。

\(\bm{0} + W\)つまり平面\(W\)も平面\(\bm{v} + W\)も平面\(\bm{v’} + W\)も\(\Reals^3 / W\)の元である。
商ベクトル空間はベクトル空間なので、\(\Reals^3 / W\)の"ベクトル"であるこれらの平面の間にも和やスカラー倍が成り立つ。

実数を係数とする変数\(x\)の多項式全体に関する商ベクトル空間

#

実数を係数とする変数\(x\)の多項式全体がそもそもベクトル空間になるの？　という方は以下の記事内の抽象ベクトル空間の記事内の具体例を読んでほしい。
🔗関連記事: 抽象ベクトル空間と部分空間の復習メモ

ベクトル空間 $$ P_n = \lbrace a_0 + a_1 x + a_2 x^2 + \dots + a_n x^n | \space a_i \in \Reals \rbrace $$ とその要素\(x^n \in P_n\)が生成する空間 $$ S[x^n] = \{ c x^n | \space c \in \Reals \} $$ を考える。

定義より、\(S[x^n]\)は\(P_n\)の部分空間である。

よって、商ベクトル空間は $$ P_n/S[x^n] = \{ [\bm{v}] | \space \bm{v} \in P_n \} = \{\bm{v} + S[x^n] | \space \bm{v} \in P_n \} \\ = \{ (a_0 + a_1 x + a_2 x^2 + \dots + a_n x^n) + S[x^n] \\ | \space (a_0 + a_1 x + a_2 x^2 + \dots + a_n x^n) \in P_n \} $$ と表すことができる。

ここで、\(a_n x^n\)と\(S[x^n]\)に着目すると、\(S[x^n]\)は\(\{ c x^n | \space c \in \Reals \}\)だったので、実質的に\(a_n x^n\)の項はなくても同じになる。

よって、最終的に $$ P_n/S[x^n] = \{ (a_0 + a_1 x + a_2 x^2 + \dots + a_{n-1} x^{n-1}) + S[x^n] \\ | \space (a_0 + a_1 x + a_2 x^2 + \dots + a_{n-1} x^{n-1}) \in P_{n-1} \} $$ となる。

\(n=2\)の場合、 $$ P_2 / S[x^2] = \{ (a_0 + a_1 x + a_2 x^2) + S[x^2] | \space (a_0 + a_1 x + a_2 x^2) \in P_2 \} \\ = \{ (a_0 + a_1 x) + S[x^2] | \space (a_0 + a_1 x) \in P_1 \} $$

ここで、\(\phi: P_2 \to \Reals^3\)という写像を $$ \phi( a_0 + a_1 x + a_2 x^2 ) = \begin{pmatrix} a_0 \\ a_1 \\ a_2 \end{pmatrix} $$ と定義すると、\(\phi\)は同型写像であり、\(\Reals^3\)を3次元空間と捉えると、空間の一点と\(P_2\)の多項式が1対1に対応する。

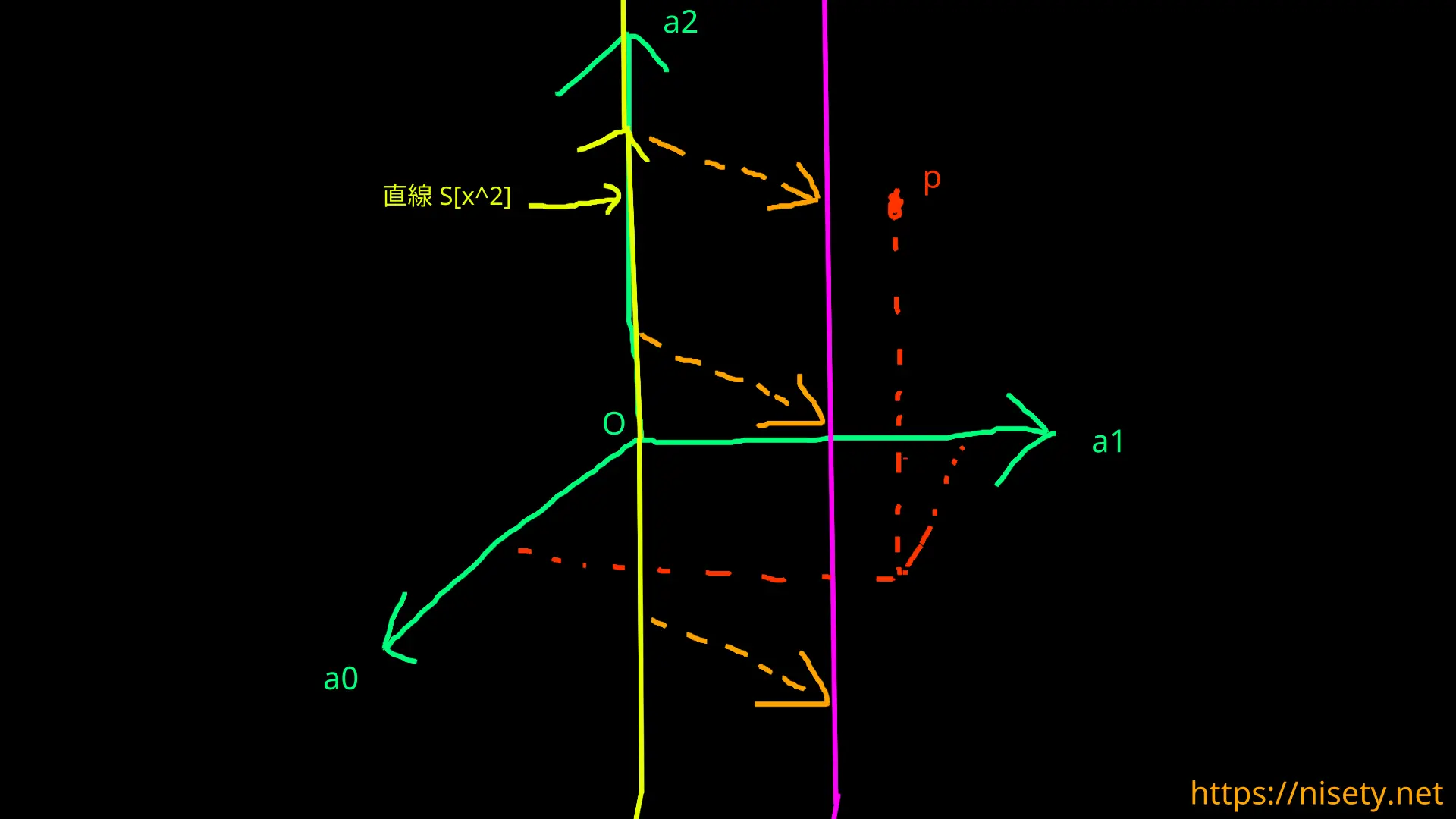
赤点pは\(a_0 + a_1 x + a_2 x^2 \)に対応する点だ。
黄色の直線は\(S[x^2]\)が張る直線。(\(x^2\)の項の係数が\(\Reals^3\)の\(a_2\)に対応するので)
ピンク色の直線は\((a_0 + a_1 x) + S[x^2]\)の一例であり、\(S[x^2]\)が\(a_0 + a_1 x\)で平行移動される様子が分かる。

平行移動しまくれば\(\Reals ^3\)が埋め尽くされることもなんとなくイメージは掴めると思う。

\(P_2 / S[x^2]\)の元は\(\Reals^3\)では直線になっていることが分かった。
更にここで、\(P_2 / S[x^2]\)の直線と\(a_0,\space a_1\)平面に着目すると、\( P_2 / S[x^2] \simeq P_1 \)(同型)である。
直線と平面の交点を考えると、\(P_1\)が\(\Reals^3\)で張る\(a_0,\space a_1\)平面の要素になっているといえばイメージできるはず。

具体例を踏まえた上で商ベクトル空間とは結局何なのか？

#

具体例から分かる通り、ベクトル空間\(V\)とその部分空間\(W\)の商ベクトル空間\(V/W\)は\(W\)の"平行移動"を一つの元とみなすことによって構成されるベクトル空間であることがわかる。

\(\Reals^3\)に同型で持ち込める場合は解釈しやすい。

上の具体例2つで、空間が埋め尽くされる様子から、\(V/W\)の元(同値類)の元(ベクトル)を全て集めたら\(V\)と一致するのではないか？　と思った人もいると思うがそのとおりである。

これが上述の同値類、商集合の性質の項で示したものが視覚化された様子だ。 $$ \underset{[x] \in V/W}{\bigcup} [x] = V $$

ベクトル空間から商ベクトル空間への自然な射影

#

ベクトル空間\(V\)とその部分空間\(W\)について、商ベクトル空間\(V/W\)を考えると、 $$ f: V \to V/W $$ という写像を考えることができる。
この写像を自然な射影(canonical projection, natural projection)という。

これは\(V\)の元(ベクトル)を\(\bm{x}\)とすると、\(\bm{x}\)が含まれる\(V/W\)の元(\([\bm{x}],\space \bm{x} + W\),同値類)への対応である。

式で表せば、 $$ f(\bm{v})=\bm{v} + W \quad (\bm{v} \in V) $$ である。

自然な射影の基本的な性質

#

上述の自然な射影\(f\)は線形写像かつ、全射である。

全射は\(f\)の定義より明らか。

線形性

#

\(V\)の任意の元\(\bm{u},\space \bm{v}\)とスカラー\(\lambda, \space \mu\)について、
$$ f(\lambda \bm{u} + \mu \bm{v}) = (\lambda \bm{u} + \mu \bm{v}) + W \\ = \lambda(\bm{u} + W) + \mu (\bm{v} + W) \\ = \lambda f (\bm{u}) + \mu f(\bm{v}) $$

自然な射影の核空間

#

\(\bm{v} \in V\)について、 $$ \small \bm{v} \in \mathrm{Ker} f \iff f(\bm{v})= \bm{0} (\in V/W) \iff [\bm{v}] = \bm{v} + W = W \iff \bm{v} \in W $$ より、\(\mathrm{Ker} f = W\)である。

universal property

#

\(V, \space W\)をベクトル空間、\(V\)の部分空間を\(S\)、\(\pi_{S}: V \to V/S\)を自然な射影、\(\mathscr{L}(V,\space W)\)を\(V \to W\)の線形写像全体とする。

\(\tau \in \mathscr{L}(V,\space W)\)が\(S \subset \mathrm{Ker} \space \tau\)を満たすとき、 $$ \gamma \circ \pi_{S} = \tau $$ を満たすuniqueな線形写像\(\gamma : V/S \to W \)が存在する。
更に、\(\mathrm{Ker} \space \gamma = \mathrm{Ker} \space \tau /S \)かつ\(\mathrm{Im} \space \gamma = \mathrm{Im} \space \tau\)である。

イメージ図

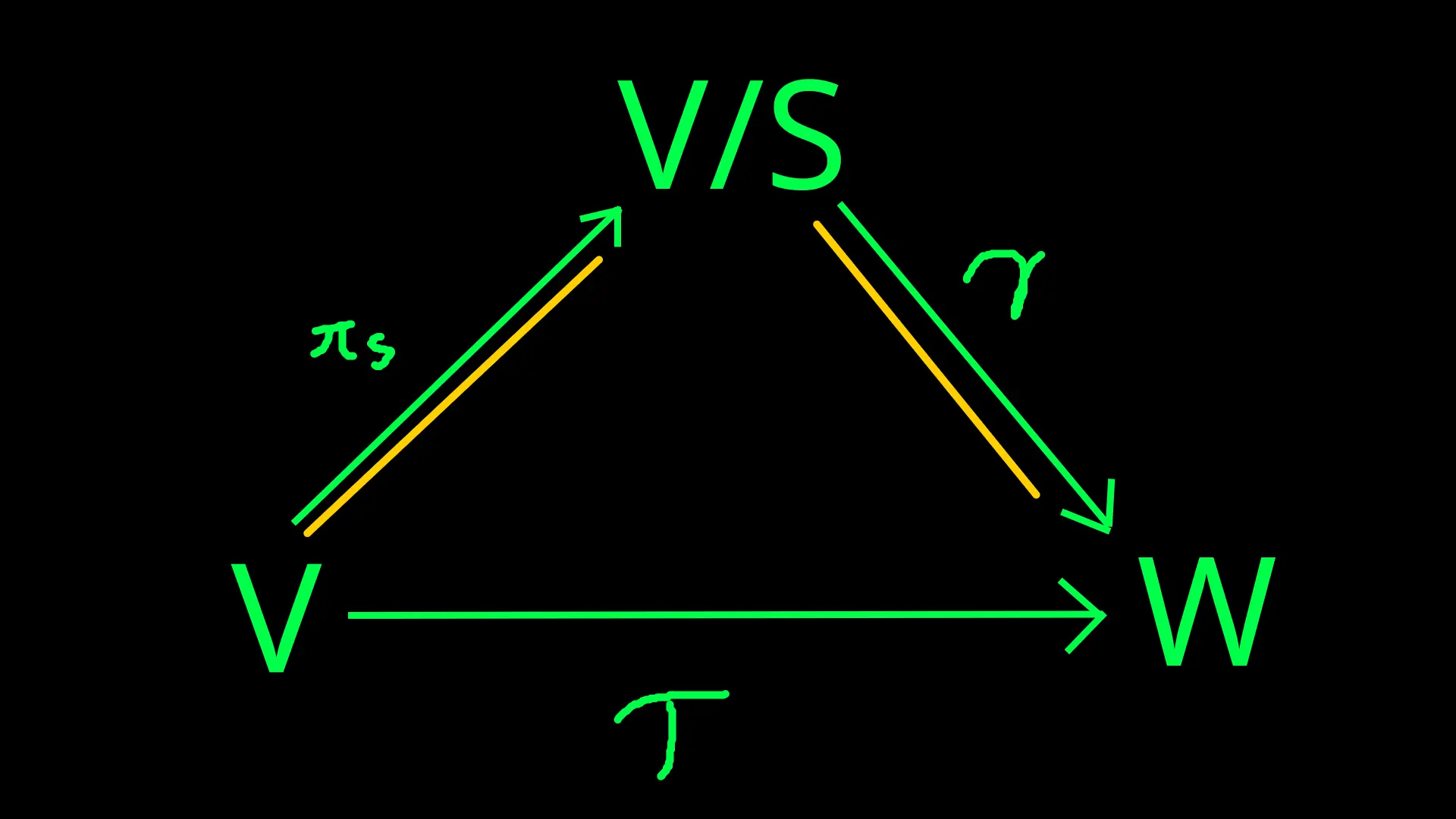
一般の場合は圏論で語られるらしい。
🔗https://en.wikipedia.org/wiki/Universal_property

証明

#

\(\gamma \circ \pi_{S} = \tau \)と\(\gamma\)を定義する。

つまり、 $$ \gamma(\bm{v} + S)=\tau(\bm{v}) \quad (\bm{v} \in V) $$ である。

この\(\gamma\)の定義には同値類が関わっているので、まず、\(\gamma\)がwell-definedであることを示さなければならない。

🔗関連記事: 同値類の演算に関して、well-defined, ill-definedとは？

$$ \bm{v} + S = \bm{u} + S \implies \gamma(\bm{v} + S) = \gamma(\bm{u}+ S) \\ (\bm{v}, \space \bm{u} \in V) \quad (q) $$ を示すことができれば、\(\gamma\)はwell-defined(代表元の取り方に依らない)といえる。

同値な条件に変形していくと、 $$ \bm{v} + S = \bm{u} + S \implies \tau(\bm{v}) = \tau(\bm{u}) \\ \bm{v} - \bm{u} \in S \implies \tau(\bm{v} - \bm{u}) = \bm{0}_W \\ \bm{x} \in S \implies \tau(\bm{x}) = \bm{0}_W \\ \Updownarrow \\ S \subset \mathrm{Ker} \space \tau $$ となる。

よって、\(\gamma\)はwell-definedである。

補足(クリックで展開)

\(\tau\)が\(S \subset \mathrm{Ker} \space \tau\)を満たすときに\(\gamma\)が存在するというのがそもそもの主張だったので、上記の変形を逆に辿れば、\(\gamma\)が存在するときに、\(\gamma\)がwell-definedということになる。

そして、
$$ \mathrm{Im} \space \gamma = \lbrace \gamma(\bm{v} + S) | \space \bm{v} \in V \rbrace = \lbrace \tau(\bm{v}) | \space \bm{v} \in V \rbrace = \mathrm{Im} \space \tau $$ より、\(\mathrm{Im} \space \gamma = \mathrm{Im} \space \tau\)が示される。

更に、 $$ \mathrm{Ker} \space \gamma = \lbrace \bm{v} + S| \space \gamma(\bm{v} + S) = \bm{0}_W \rbrace \\ = \lbrace \bm{v} + S| \space \tau(\bm{v}) = \bm{0}_W \rbrace \\ = \lbrace \bm{v} + S| \space \bm{v} \in \mathrm{Ker} \space \tau \rbrace \\ = \mathrm{Ker} \space \tau / S $$ より、\(\mathrm{Ker} \space \gamma = \mathrm{Ker} \space \tau / S\)が示される。(最後の変形は商ベクトル空間の定義そのもの。)

\(\gamma\)がuniqueなことは\(\gamma\)の定義から明らか。

\(\gamma\)を適当な\(\gamma\)でない写像で入れ替えても最終的にその写像は\(\gamma\)と等しくなるはず。
関連記事 Proving a linear transformation is unique: 🔗https://math.stackexchange.com/questions/3263742/proving-a-linear-transformation-is-unique

商ベクトル空間の基底と次元

#

\(V\)をベクトル空間、\(W\)をその部分空間とすると、\(V/W\)の次元は $$ dim \space (V/W)= dim \space V - dim \space W $$ となる。

証明

#

\(n = dim \space V, \space m = dim \space W \)とする。

\(W\)の1組の基底\(\bm{w}_1, \space \dots , \bm{w}_m \)を基底の延長定理を適用して延長して\(V\)の基底

$$ \bm{w}_{1}, \space \dots , \space \bm{w}_{m} , \space \bm{v}_{m+1}, \space \dots , \space \bm{v}_{n} $$ を得る。

このとき

$$ \bm{v}_{m+1} + W, \space \bm{v}_{m+2} + W , \space \dots , \space \bm{v}_{n} + W $$ が\(V/W\)の基底になることを示す。

任意の\(\bm{v} + W \in V/W \)を一次結合(線形結合)で表せる

#

\(\bm{w}_{1}, \space \dots , \space \bm{w}_{m} , \space \bm{v}_{m+1}, \space \dots , \space \bm{v}_{n}\)は\(V\)の基底なので適当な\(a_0, \dots, a_n\)で、
$$ \bm{v} + W =( a_0 \bm{w}_{1} + \dots + a_m \bm{w}_{m} + a_{m+1} \bm{v}_{m+1} + \dots + a_n \bm{v}_{n} ) + W $$ と表すことができる。

さらに変形していくと、
$$ =\{ ( a_0 \bm{w}_{1} + \dots + a_m \bm{w}_{m}) + W \} + \{ (a_{m+1} \bm{v}_{m+1} + \dots + a_n \bm{v}_{n} ) + W \} $$ となり、\(( a_0 \bm{w}_{1} + \dots + a_m \bm{w}_{m}) \in W\)と\( \bm{w} \in W \iff \bm{w} + W = W\)より、 $$ = W + (a_{m+1} \bm{v}_{m+1} + \dots + a_n \bm{v}_{n} ) + W $$ となる。

\(W\)の演算が閉じていることを考え、更に変形していくと、
$$ = (a_{m+1} \bm{v}_{m+1} + \dots + a_n \bm{v}_{n} ) + W \\ = a_{m+1} (\bm{v}_{m+1} + W ) + \dots + a_n (\bm{v}_{n} + W) $$ となり、\(\bm{v} + W\)は\(\bm{v}_{m+1} + W , \space \dots , \space \bm{v}_{n} + W \)の一次結合で表せることが示される。

最後の式変形についての補足(クリックで展開)

一応だが、\(\bm{v} + W\)は(抽象)ベクトルの集合である。

画像の左側が\((a_{m+1} \bm{v}_{m+1} + \dots + a_n \bm{v}_{n} ) + W\)の例で、
右側が\(a_{m+1} (\bm{v}_{m+1} + W ) + \dots + a_n (\bm{v}_{n} + W)\)の例である。

右側から左側へ持っていくのは難しいので、左側を変形して右側に持っていくことを考える。

左側の例えば、\(\bm{w}_1\)が現れた元に着目する。
この元に対応する右側の元は最初の\(W\)の項が\(\bm{w}_1\)でその他の項の\(W\)が全てゼロベクトルである場合が考えられるので、左側の元は全て右側に存在することになる。

つまり、 $$ (a_{m+1} \bm{v}_{m+1} + \dots + a_n \bm{v}_{n} ) + W \subset a_{m+1} (\bm{v}_{m+1} + W ) + \dots + a_n (\bm{v}_{n} + W) $$ である。

そして、強引に感じるが、\(W\)の演算が閉じていることを考えると、左の元で各々の項の\(W\)がどのような元であっても、画像の右側のようにスカラー倍と和でまとめることができて、その結果は\(\in W\)なので結局集合として左側と右側は等しくなる。

ベクトル空間が閉じていることがまさかここまで強力だとは。

一次独立(線形独立)である

#

\(a_{i}\)をスカラーとして、一次関係を考えると
$$ a_{m+1} (\bm{v}_{m+1} + W) + \dots + a_{n} (\bm{v}_{n} + W) = W $$ である。

しつこいようだが、\(V/W\)のゼロベクトルは\(W\)だ。

変形すると、 $$ a_{m+1} \bm{v}_{m+1} + \dots+ a_{n} \bm{v}_{n} + W = W $$ となるので、\(a_{m+1} \bm{v}_{m+1} + \dots+ a_{n} \bm{v}_{n} \in W\)である。

この変形が分からなければ、一つ前の項にも登場しているのでそちらを見てほしい。

よって、ある\(\bm{w} \in W\)で $$ a_{m+1} \bm{v}_{m+1} + \dots+ a_{n} \bm{v}_{n} = \bm{w} $$ となり、右辺を\(W\)の基底\(\bm{w}_1, \space \dots, \bm{w}_{m}\)の一次結合で表すと、
$$ a_{m+1} \bm{v}_{m+1} + \dots+ a_{n} \bm{v}_{n} = a_1 \bm{w}_1 + \dots + a_{m} \bm{w}_{m} \\ - a_1 \bm{w}_1 + \dots - a_{m} \bm{w}_{m} + a_{m+1} \bm{v}_{m+1} + \dots+ a_{n} \bm{v}_{n} = \bm{0} $$ となる。

いま、左辺は\(V\)の基底の一次結合になっているので、基底の一次独立性より、係数\(a_{i}\)は全て\(0\)である。

よって、一次独立であることが示された。

以上によって $$ \bm{v}_{m+1} + W, \space \bm{v}_{m+2} + W , \space \dots , \space \bm{v}_{n} + W $$ が\(V/W\)の基底であることが示された。

よって、\(dim \space (V/W) = dim \space V - dim \space W \) である。

実は、\(n\)次元のベクトル空間に関して、\(n\)個のベクトルの一次独立性か空間を生成することどちらかを示せば基底といえるが、一応、両方記述しておいた。

線形写像の核空間と像空間、商ベクトル空間の関係

#

線形写像\(f: V \to W\)について、\(\phi: V/ \mathrm{Ker} f \to \mathrm{Im} f\), $$ \phi(\bm{v} + \mathrm{Ker} f) = f(\bm{v}) $$ とすると、\(\phi\)は同型写像である。
つまり、\( V/ \mathrm{Ker} f \cong \mathrm{Im} f\)である。

証明

#

\(\phi\)がwell-definedかつ全単射かつ線形写像であることを示せば良い。

\(\phi\)はwell-definedである

#

\(\bm{v} + \mathrm{Ker} f\)の異なる代表元\(\bm{x}, \space \bm{y} \in \bm{v} + \mathrm{Ker} f \)に関して、
\(\phi(\bm{x}) = \phi(\bm{y})\)を示す。

\(\bm{x}, \space \bm{y}\)はそれぞれ\(\bm{v} + \mathrm{Ker} fのベクトル\) の形で表せることと、\(\mathrm{Ker} f\)は部分空間であり、和に関して閉じていること、\(\phi(\bm{v} + ( \bm{k} \in \mathrm{Ker} f)) = f(\bm{v})\)に注意して、 $$ \phi(\bm{x})=\phi(\bm{x} - \bm{y} +\bm{y} ) \\ = f(\bm{v} - \bm{v} + \bm{v}) \\ = f(\bm{v} - \bm{v}) + f(\bm{v}) \\ = f(\bm{0}) + f(\bm{v}) \\ = f(\bm{v}) \\ = \phi(y) $$

\(\phi\)は全射

#

任意の\(\bm{v} \in \mathrm{Im} f\)について、\(\mathrm{Im} f\)の定義より、\(\exists \bm{v’} \in V, \space f(\bm{v’})=\bm{v}\)である。

このとき、\(\phi(\bm{v’} + \mathrm{Ker} f) = f(\bm{v’})=\bm{v}\)なので\(\phi\)は全射である。

\(\phi\)は単射

#

\(\phi(\bm{v} + \mathrm{Ker} f) = \phi(\bm{v’} + \mathrm{Ker} f)\)と仮定する。

このとき、\(\phi\)の定義より\(f(\bm{v}) = f(\bm{v’})\)であり、\(f\)の線形性より、 $$ f(\bm{v} - \bm{v’}) = \bm{0} $$

よって、\(\bm{v} - \bm{v’} \in \mathrm{Ker} f\)であり、\(\bm{v} \in \bm{v’} + \mathrm{Ker} f\)なので、\(\bm{v} + \mathrm{Ker} f = \bm{v’} + \mathrm{Ker} f\)であり、\(\phi\)は単射である。

\(\phi\)は線形写像

#

\(\lambda,\space \mu \in K\), \(\bm{v} + \mathrm{Ker} f, \space \bm{v’} + \mathrm{Ker} f \in V/W\)に対して、 $$ \phi (\lambda(\bm{v} + \mathrm{Ker} f)+ \mu(\bm{v’} + \mathrm{Ker} f))= \phi(\lambda \bm{v}+\mu \bm{v’} + \mathrm{Ker} f) \\ = f(\lambda \bm{v}+\mu \bm{v’}) \\ = \lambda f(\bm{v}) + \mu f (\bm{v’}) \\ = \lambda \phi(\bm{v} + \mathrm{Ker} f) + \mu \phi (\bm{v’} + \mathrm{Ker} f) $$ なので、\(\phi\)は線形写像である。

以上より、\(\phi\)が同型写像であることが示された。

線形写像の基本定理(線形写像の次元定理)

#

\(V,\space W\)をベクトル空間とする。 線形写像\(f: V \to W\)に対して、 $$ dim \space V = dim \space \mathrm{Im} f + dim \space \mathrm{Ker} f $$ が成り立つ。

一応、この定理は商ベクトル空間を用いなくても、\(\mathrm{Ker} f\)の基底と\(\mathrm{Im} f\)の基底に対応する\(V\)のベクトルたちが\(V\)の基底になることを示すことによって証明できる。

証明

#

$$ dim \space (V/\mathrm{Ker} f) = dim \space V - dim \space \mathrm{Ker} f \\ = dim \space \mathrm{Im} f \space \because V/\mathrm{Ker} f \cong \mathrm{Im} f $$

よって、 $$ dim \space V= dim \space \mathrm{Im} f + dim \space \mathrm{Ker} f $$

編集後記

#

商ベクトル空間自体の概要は少し理解できたが、その前に何を学んでいる途中だったのか忘れてしまった。

冒頭の動機に残ってたがそんなことしてたっけ…。

商ベクトル空間の具体例では\(\Reals^3\)関連しか扱わなかったが、もっと次元が高い例だともしかしたら超平面とかいうやつが関係してくるのかな？

n-1次元の"平面"の平行移動で空間が埋め尽くされるとか？ 分からんが。
空間が直線の平行移動で埋め尽くされる具体例もあるからn-1とは限らなそうだし。

そのうち🔗hyper plane(wikipedia)辺りを少し読んで考えておきたい。

追記(2024-05-02): 自然な射影の核空間の項で線形写像\(V \to V/W\)の核空間が\(W\)であることが分かったが、これが商ベクトル空間 は\(W\)を"一点"に潰して得た空間と言われる所以だろうか？
一点と言っても、\(V/W\)の"ゼロベクトル"は\(W\)だが。

参考文献

#

1. 🔗線形代数学 (川久保勝夫 著)
2. 🔗A First Course In Linear Algebra (Robert A Beezer 著)
3. 🔗理工系の基礎線形代数学 (硲野 敏博, 加藤 芳文 著)
4. 🔗線形空間論入門 (明松 真司 著)
5. 🔗Linear Algebra (Sterling K. Berberian 著)
   🔗同じ著者から2013年発売の線形代数の本が出ているのでそちらのほうが良いかもしれない。
6. 🔗現代ベクトル解析の原理と応用 (新井 朝雄 著)
7. 🔗Advanced Linear Algebra (Graduate Texts in Mathematics) (Steven Roman 著)