線形変換 #
\(V,W\)を複素数体上の(スカラーとして複素数を考える)ベクトル空間とする。
線形変換とは、線形写像の定義域(domain)、値域(codomain)が両方同じベクトル空間のもののことをいう。
つまり、一例として、線形写像\(f: V \to V\)、\(g: W \to W\)のようなものが線形変換だ。
余談だが、線形写像、線形変換全体をまとめて表す記号が使われていることがあるので紹介しておく。
\(\mathscr{L}(V)\)は定義域、値域が\(V\)である線形変換全体の集合、
\(\mathscr{L}(V,\space W)\)は定義域\(V\)、値域が\(W\)である線形写像全体の集合を表す。
この記法はめちゃんこ便利だ。
一応latex表記も載せておく。
\mathscr{L}(V,\space W)
固有値、固有ベクトル #
\(V\)をベクトル空間とする。
線形変換\(f: V \to V\)について、 $$ f(\bm{v}) = \lambda \bm{v} \quad \bm{v} \in V, \space \bm{v} \neq \bm{0}, \space \lambda \in \Complex $$ を満たす\(\lambda\)を\(f\)の固有値、\(\bm{v}\)を固有値\(\lambda\)に関する固有ベクトルという。
固有値の場合は\(0\)を値として許すが、固有ベクトルに関しては\(\bm{0}\)(ゼロベクトル)を固有ベクトルと認めない。
定義はカンタンだ。
\(f\)の表現行列を\(A_{f}\)とすると、 $$ A_{f} \bm{v} = \lambda \bm{v} $$ と表すこともできる。
一般のベクトル空間の線形変換についての固有値の議論について #
ただ、上式の\(A_{f} \bm{v}\)内の\(\bm{v}\)は\(V\)のベクトルではなくて、\(\bm{v}\)の成分ベクトル(数ベクトル)であることに注意。
ベクトル空間の公理では、行列と一般のベクトルの積は定義されていない。
しかし、数ベクトル空間のみに焦点を当てて固有値の議論をしても差し支えがない(むしろ簡単なので良い)ことが分かる。
なぜなら、行列とベクトルの積が定義されていない、一般のベクトル空間の固有値(やその関連)について考える場合は、直接ベクトル空間のベクトルについて論じるのではなく、🔗線形変換を得る際に固定した基底に関する成分ベクトル(あるベクトル\(\bm{v} \in V\)を\(V\)のある基底の一次結合で表したときの係数のスカラーをまとめて数ベクトルにしたもの)である、数ベクトルに関して議論すれば良いだけだからだ。
視覚化 #
例えばベクトル空間として\(\Reals^2\)を考えて適当に視覚化すると、固有ベクトル\(\bm{v}\)を\(f\)で写した結果は\(\lambda\)倍になるだけなので、以下のように同直線上に存在することがわかる。
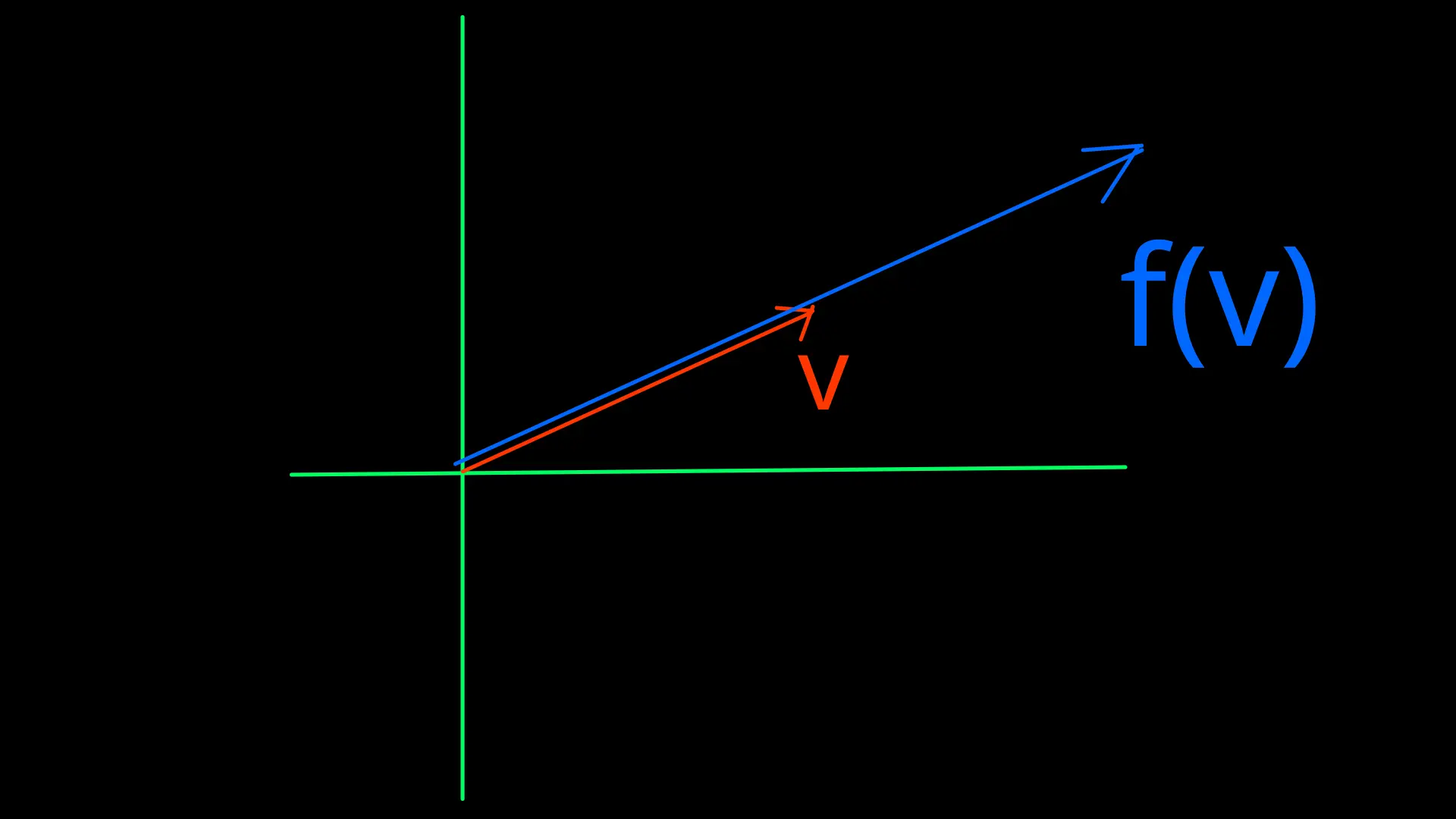
固有空間 #
ベクトル空間\(V\)と線形変換\(f: V \to V\)の固有値の一つを\(\lambda\)とするとき、 \(\lambda\)に関する固有ベクトルの全体とゼロベクトルからなる集合を\(f\)の固有値\(\lambda\)に属する固有空間という。
$$ \lbrace \bm{v} \in V | \space f(\bm{v}) = \lambda \bm{v} \rbrace $$
固有ベクトルに\(\bm{0}\)は含まれないが、固有空間には含まれることに注意。
\(f\)の線型性と固有ベクトルの定義より、固有空間は\(V\)の部分空間であることが示される。
固有多項式 #
\(n\)次元正方行列\(A\)に関して $$ \phi_{A}(t) := | A - tE| $$ と定義される\(t\)の多項式\(\phi_{A}(t)\)を固有多項式、特性多項式(characteristic polynomial)といい、\(\phi_{A}(t) = 0\)を固有方程式という。
また、固有方程式の解(固有値)の重複度を固有値の重複度という。
線形変換\(f: V \to V\)が与えられたとき、\(\lambda\)が\(f\)の固有値であるための必要十分条件は $$ \phi_{A_{f}}(\lambda) = | A_{f} - \lambda E | = 0 $$ つまり、\(\lambda\)が固有方程式の解であることである。
証明 #
固有値の定義より、\(A_{f} \bm{v} = \lambda \bm{v} \quad \bm{v} \in V\)。
この等式を変形することによって証明する。 $$ A_{f} \bm{v} = \lambda \bm{v} \\ A_{f} \bm{v} - \lambda \bm{v} =\bm{0} \\ A_{f} \bm{v} - \lambda E \bm{v} =\bm{0} \quad Eは単位行列 \\ (A_{f} - \lambda E)\bm{v} =\bm{0} $$
行列の計算則 (KIT(金沢工業大学)数学ナビゲーション)
🔗https://w3e.kanazawa-it.ac.jp/math/category/gyouretu/senkeidaisu/henkan-tex.cgi?target=/math/category/gyouretu/senkeidaisu/gyouretu_no_keisan.html
つまり、\(\lambda\)が固有値であるということと、\((A_{f} - \lambda E)\bm{v} =\bm{0}\)が非自明解\(\bm{v} \neq \bm{0}\)をもつことは同値であることが判明する。
このことから、固有空間は\((A_{f} - \lambda E)\bm{v} =\bm{0}\)の解空間であることも判明する。
\((A_{f} - \lambda E)\)の核空間ともいえる。
\((A_{f} - \lambda E)\bm{v} =\bm{0}\)は連立斉一次方程式なので、🔗連立斉一次方程式(斉次連立一次方程式)が非自明な解をもつ条件の大まかなイメージより、非自明解をもつのは $$ | A_{f} - \lambda E | = 0 $$ のときであることがわかる。
固有値、固有ベクトルの存在 #
実数体上のベクトル空間の線形変換について考えている場合は、実数の範囲で常に固有方程式が解をもつとは限らない。
複素数体上の場合は、代数学の基本定理より複素数の範囲では必ず固有方程式の解が存在するので常に固有値が存在する。(つまり、定義より固有ベクトルも存在する。)
固有値の重複度 #
固有値には二種類の重複度が定義されている。
固有値の代数的重複度(algebraic multiplicity) #
代数的重複度は固有多項式\(\phi_{A}(t)\)の根の重複度のこと。
「根」と「解」は同じですか: 🔗https://math.hyuki.net/20190506210952/
つまり、固有値\(\lambda\)の代数的重複度とは\(\phi_{A}(t)\)を因数分解したときに\((t-\lambda)\)が現れる回数である。
固有値の幾何的重複度(geometric multiplicity) #
固有値\(\lambda\)の幾何的重複度とは\(\lambda\)に属する固有空間\(V(\lambda)\)の次元\(\dim V(\lambda)\)のことである。
具体例: 固有値、固有空間の求め方 #
せっかくなのでここで、ここまで登場した事柄の具体例を求めてみることにする。
\(V\)を3項数ベクトル空間とする。
スカラーとしては実数を考える。
線形変換\(f: V \to V\)の表現行列を\(A_f = \begin{pmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 2 & 0 \end{pmatrix}\)とする。
まず、固有多項式を求める。
$$ \phi_{A_{f}}(t) = |A_f - t E| = \begin{pmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 2 & 0 \end{pmatrix} - \begin{pmatrix} t & 0 & 0 \\ 0 & t & 0 \\ 0 & 0 & t \end{pmatrix} \\ = \begin{pmatrix} 1 -t & 0 & 1 \\ 0 & 1-t & 1 \\ 1 & 2 & -t \end{pmatrix} $$
次に、固有値を求めるために、固有方程式を解く。 $$ \phi_{A_{f}}(t) = 0 \\ \begin{vmatrix} 1 -t & 0 & 1 \\ 0 & 1-t & 1 \\ 1 & 2 & -t \end{vmatrix} = 0 \\ (1-t)(1-t)(-t) -(1-t) - 2(1-t) = 0 \\ (1-t) \lbrace -t(1-t) - 1 -2 \rbrace =0 \\ (1-t)(t^2 -t -3) = 0 \\ t = 1, \space \frac{1 \pm \sqrt{13} }{2} $$
よって、固有値は\(1, \space \frac{1 \pm \sqrt{13} }{2}\)となる。
固有値が全部整数になるように簡単そうな行列を選んだがうまくいかなくて絶望した。
固有値を求めることができたので、固有空間を求める。
固有値\(1\)に属する固有空間を求めよう。
固有空間は $$ (A_{f} - t E)\bm{x} =\bm{0} \quad \bm{x} \in V $$ を満たす固有ベクトル\(\bm{x}\)の全体と\(\bm{0}\)からなる集合なので、 $$ (A_{f} - 1 E)\bm{x} = \bm{0} \\ \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 2 & -1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$
を満たす\(\bm{x}\)の成分\(x_1, \space x_2, \space x_3\)がどんなものかを調べれば良い。
左辺の積を計算すると、 $$ \begin{pmatrix} x_3 \\ x_3 \\ x_1 + 2 x_2 - x_3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$ となるので、\(\bm{x}\)の成分の間には $$ x_3 = 0 \\ x_1 + 2 x_2 - x_3 = 0 \implies 2 x_2 = - x_1 $$ という関係があることがわかる。
つまり、\(1\)に属する固有空間の固有ベクトルは上の関係さえ満たしていれば良いのだから $$ \lbrace r \begin{pmatrix} -2 \\ 1 \\ 0 \end{pmatrix} | \space r \in \Reals \rbrace $$ と固有空間を求めることができる。
この固有空間の次元は\(1\)である。
もちろん、他の固有値に属する固有空間も同様の計算手順で求めることができる。
固有ベクトルの一次独立性 #
\(n\)次正方行列\(A\)の相異なる固有値を $$ \lambda_1, \space \dots, \space \lambda_{k} \quad (k \leqq n) $$ とする。
各固有値\(\lambda_{i}\)に属する(固有空間の)固有ベクトルを\(\bm{x}_{i}\)とするとき、\(\bm{x}_1, \space \dots, \space \bm{x}_{k}\)は一次独立である。
証明 #
固有ベクトルは\(\bm{0}\)でないので、\(\bm{x}_1\)は一次独立である。
これに他の固有ベクトルを追加したものが一次独立であることを背理法を用いて示す。
\(j < k\)を満たすある\(j\)を用いて、\(\bm{x}_{1}, \space \dots, \space \bm{x}_{j}\)が一次独立であるとき、 \(\bm{x}_{1}, \space \dots, \space \bm{x}_{j}, \space \bm{x}_{j+1}\)が一次従属になると仮定する。
このとき、\(\bm{x}_{j+1}\)は $$ \bm{x}_{j+1}=a_1 \bm{x}_{1} + \dots + a_{j} \bm{x}_j \quad (1) $$ と表される。
補足:
一次独立、一次従属の性質。
\(s+1\)個のベクトルが一次従属で、\(s\)個のベクトルが一次独立なとき、取り除いたひとつのベクトルは\(s\)個のベクトルの一次結合で一意的に表されることが知られている。
\(\bm{x}_{j+1}\)は固有ベクトルなので、\(\bm{x}_{j+1} \neq \bm{0}\)であることから、 \(\bm{x}_{j+1}=a_1 \bm{x} + \dots + a_{j} \bm{x}_j \)の右辺のスカラー\(a_1, \space \dots, \space a_{j}\)の中に少なくともひとつ、\(0\)でないものが存在する。
\(\bm{x}\)を列ベクトルとして、\(A\)を\((1)\)の両辺に左からかけると、 $$ A \bm{x}_{j+1}= a_1 A \bm{x}_{1} + \dots + a_{j} A \bm{x}_j $$ を得る。
\(\bm{x}_{i}\)は固有ベクトルなので\(A\bm{x}_{i}=\lambda_{i}\bm{x}_{i}\)であることに注意して変形すると、
$$ \lambda_{j+1} \bm{x}_{j+1}= a_1 \lambda_{1} \bm{x}_{1} + \dots + a_{j} \lambda_{j} \bm{x}_j \quad (2) $$ を得る。
そして、\((1)\)の等式の両辺に\(\lambda_{j+1}\)をかけて $$ \lambda_{j+1}\bm{x}_{j+1}= a_1 \lambda_{j+1} \bm{x}_{1} + \dots + a_{j} \lambda_{j+1} \bm{x}_j \quad (3) $$ を得る。
\((2),\space (3)\)より、 $$ \bm{0} = a_{1} (\lambda_{1} - \lambda_{j+1})\bm{x}_{1} + \dots + a_{j} (\lambda_{j} - \lambda_{j+1})\bm{x}_{j} $$
仮定より\(\lambda_{i}\)は全て異なるので、\(\lambda_{i} - \lambda_{j+1} \neq 0\)であり、その上先程、\(a_1, \space \dots, \space a_{j}\)の中に少なくともひとつ、\(0\)でないものが存在することが示されている。
これは、\(\bm{x}_{1}, \space \dots, \space \bm{x}_{j}\)が一次独立あるという仮定に反する。
よって、\(\bm{x}_1, \space \dots, \space \bm{x}_{k}\)は一次独立である。
相似な行列と固有値 #
線形変換\(f: V \to V, \space g: V \to V\)の表現行列の正方行列\(A_{f}, \space B_{g}\)が以下のように相似 $$ B_{g} = P^{-1}A_{f}P \quad (Pはある正則行列) $$ の関係にあるとき、\(\phi_{A_{f}}(t) = \phi_{B_{g}}(t)\)であり、\(f,\space g\)の固有値全体は一致する。
証明 #
$$ \phi_{B_{g}}(t) = | B_{g} - tE|= |P^{-1}A_{f}P - tE| $$
\(tE\)は単位行列の定義より、任意の行列に対して可換(積の順番を入れ替えられる)なので、
$$ |P^{-1}A_{f}P - tE| = |P^{-1} A_{f}P- P^{-1} tE P| \\ = |P^{-1}(A_{f}P- tE P)| = |P^{-1}(A_{f}- tE)P| \\ = |P^{-1}||A_{f}- tE||P| = |P^{-1}||P||A_{f}- tE| \\ = |P^{-1} P||A_{f}- tE| = |E||A_{f}- tE| = |A_{f}- tE| = \phi_{A_{f}}(t) $$
よって、\(\phi_{A_{f}}(t) = \phi_{B_{g}}(t)\)である。
したがって、固有値も一致する。
線形変換の固有多項式は基底の取り方に依らない #
🔗基底の取り替えと線形写像の表現行列の関係より、線形変換を行列表示したときに、基底を取り替えて得た表現行列ともとの表現行列は相似の関係になる。
よって、上述の相似な行列と固有値で示された事実より、それらの行列の固有多項式は一致する。
当然だが、固有多項式が一致するので固有値も一致する。
一般のベクトル空間に関する固有値、固有空間、固有ベクトルの具体例 #
先程具体例を記述したが、そちらで具体的なベクトルを扱っておらず、本当に固有値関連の概念が一般のベクトル空間の公理から導かれる演算や性質だけで構築できるのか理解してスッキリさせておきたいと思ったので。
今度は一般のベクトル空間の具体例として、\(2 \times 2\)行列全体からなるベクトル空間を\(V\)を考える。
なお、スカラーとしては実数を考える。(実数体上のベクトル空間)
\(\dim V = 4\)である。
なぜ\(\dim V = 4\)なのか別記事で触れている箇所があったのでリンクしておく。
🔗link
まず、線形変換を得るところから始めよう。
\(V\)の基底として、 $$ \begin{pmatrix} 1 & 0 \\ 0 & 0 \\ \end{pmatrix}, \space \begin{pmatrix} 0 & 1 \\ 0 & 0 \\ \end{pmatrix}, \space \begin{pmatrix} 0 & 0 \\ 1 & 0 \\ \end{pmatrix}, \space \begin{pmatrix} 0 & 0 \\ 0 & 1 \\ \end{pmatrix} $$ を固定する。
線形変換\(f: V \to V\)がベクトル $$ \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} $$ を $$ \begin{pmatrix} d & c \\ b & a \\ \end{pmatrix} $$ に写すとする。
\(f\)の表現行列を\(A_{f}\)とすると、 $$ \begin{pmatrix} d \\ c \\ b \\ a \end{pmatrix} = A_{f} \begin{pmatrix} a \\ b \\ c \\ d \end{pmatrix} $$ という関係を得られる。
なぜ基底を固定したのか、なぜ上述の関係が得られるのかが分からなければ以下を参照してほしい。
🔗抽象ベクトル空間の間の線形写像とその表現行列
\(A_{f}\)を成分で表して計算して解く $$ \begin{pmatrix} d \\ c \\ b \\ a \end{pmatrix} = \begin{pmatrix} r_{11} & r_{12} & r_{13} & r_{14} \\ r_{21} & r_{22} & r_{23} & r_{24} \\ r_{31} & r_{32} & r_{33} & r_{34} \\ r_{41} & r_{42} & r_{43} & r_{44} \end{pmatrix}\begin{pmatrix} a \\ b \\ c \\ d \end{pmatrix} \\ = \begin{pmatrix} r_{11} a + r_{12} b + r_{13} c + r_{14} d \\ r_{21} a + r_{22} b + r_{23} c + r_{24} d \\ r_{31} a + r_{32} b + r_{33} c + r_{34} d \\ r_{41} a + r_{42} b + r_{43} c + r_{44} d \end{pmatrix} $$ 最初のベクトルと最後のベクトルの行を比較して、 $$ A_{f} = \begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix} $$ であることが分かる。
具体的な表現行列が分かったので、固有値、固有ベクトル、固有空間を求めてみよう。
まず、固有値を求めるために固有方程式を解く。 $$ \phi_{A_{f}} = 0 \\ | A_{f} - tE | = 0 \\ \left| \begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix} - \begin{pmatrix} t & 0 & 0 & 0 \\ 0 & t & 0 & 0 \\ 0 & 0 & t & 0 \\ 0 & 0 & 0 & t \end{pmatrix} \right| = 0 \\ \begin{vmatrix} -t & 0 & 0 & 1 \\ 0 & -t & 1 & 0 \\ 0 & 1 & -t & 0 \\ 1 & 0 & 0 & -t \end{vmatrix} = 0 $$
これを解いて\(t\)を求めたいのだが、流石に\(4 \times 4\)はやばいので行列式の性質を使って楽をする。
1列目に\(t\)をかけた結果を4列目に足しても行列式の値は変わらないので、 $$ \begin{vmatrix} -t & 0 & 0 & 1 - t^2 \\ 0 & -t & 1 & 0 \\ 0 & 1 & -t & 0 \\ 1 & 0 & 0 & 0 \end{vmatrix} = 0 $$ 1列目と4列目を入れ替えると、行列式の値は\(-1\)倍になるので、 $$ (-1) \begin{vmatrix} 1 - t^2 & 0 & 0 & -t\\ 0 & -t & 1 & 0 \\ 0 & 1 & -t & 0 \\ 0 & 0 & 0 & 1 \end{vmatrix} = 0 $$ となり、1列目に注目すると\((2,1) (3,1) (4,1)\)が全て\(0\)なので、 $$ (-1)(1-t^2) \begin{vmatrix} -t & 1 & 0 \\ 1 & -t & 0 \\ 0 & 0 & 1 \end{vmatrix} = 0 $$ となる。
更に、1行目と3行目を入れ替えた後、1列目と3列目を入れ替えて、 $$ (-1)(1-t^2) \begin{vmatrix} 1 & 0 & 0 \\ 0 & -t & 1 \\ 0 & 1 & -t \end{vmatrix} = 0 \\ (-1)(1-t^2)(1) \begin{vmatrix} -t & 1 \\ 1 & -t \end{vmatrix} = 0 \\ (t^2 -1)(t^2 -1)=0 $$ よって、\(t=\pm 1 \space (\pm \sqrt{1}) \)なので、固有値は\(\pm 1\)である。
例として、固有値\(-1\)について、属する固有空間と固有ベクトルの具体的な値を調べよう。
固定した基底の一次結合で\(V\)のあるベクトルを表すと、\(\dim V = 4\)より、成分ベクトルとして4項数ベクトルを得ることができる。
固有空間は $$ (A_{f} - (-1)E) \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\x_4 \end{pmatrix} =\bm{0} $$ を満たす数ベクトルを先程固定した基底に関する成分ベクトルとする、ベクトル $$\bm{v} = x_1 \begin{pmatrix} 1 & 0 \\ 0 & 0 \\ \end{pmatrix} + x_2 \begin{pmatrix} 0 & 1 \\ 0 & 0 \\ \end{pmatrix} + x_3 \begin{pmatrix} 0 & 0 \\ 1 & 0 \\ \end{pmatrix} + x_4 \begin{pmatrix} 0 & 0 \\ 0 & 1 \\ \end{pmatrix} \\ \bm{v} \in V $$ の集まりである。
$$ (\begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix} + 1 E) \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\x_4 \end{pmatrix} = \bm{0} \\ \begin{pmatrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\x_4 \end{pmatrix} = \bm{0} \\ \begin{pmatrix} x_1 + x_4 \\ x_2 + x_3 \\ x_2 + x_3 \\ x_1 + x_4 \end{pmatrix} = \bm{0} $$
つまり、\(x_1 = - x_4\)かつ\(x_2 = - x_3\)である。
よって\(V\)の固有値\(-1\)に属する固有空間は\(a,\space b\)を任意のスカラーとして $$ a \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} + b \begin{pmatrix} 0 \\ 1 \\ -1 \\ 0 \end{pmatrix} $$ と表すことができる数ベクトルを固定した基底に関する成分ベクトルとするベクトルの全体とゼロベクトルからなる部分空間である。
具体的な固有空間の元は、例えば\(a = 3, \space b=-2\)の場合、成分ベクトルが $$ 3 \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} -2 \begin{pmatrix} 0 \\ 1 \\ -1 \\ 0 \end{pmatrix} \\ = \begin{pmatrix} 3 \\ 0 \\ 0 \\ -3 \end{pmatrix} + \begin{pmatrix} 0 \\ -2 \\ 2 \\ 0 \end{pmatrix} \\ = \begin{pmatrix} 3 \\ -2 \\ 2 \\ -3 \end{pmatrix} $$ であり、 $$ 3 \begin{pmatrix} 1 & 0 \\ 0 & 0 \\ \end{pmatrix} -2\begin{pmatrix} 0 & 1 \\ 0 & 0 \\ \end{pmatrix} + 2 \begin{pmatrix} 0 & 0 \\ 1 & 0 \\ \end{pmatrix} -3 \begin{pmatrix} 0 & 0 \\ 0 & 1 \\ \end{pmatrix} = \begin{pmatrix} 3 & -2 \\ 2 & -3 \\ \end{pmatrix} $$ となる。