上界、下界

上界、下界
#

順序集合$(P,\space \leqq)$とその部分集合$Q$に関して $$ p \in P \land \forall q \in Q,\space q\leqq p $$ である$p$を$Q$の 上界(upper bound) という。

対して、 $$ p \in P \land \forall q \in Q,\space q\geqq p $$ である$p$を$Q$の 下界(lower bound) という。

上界が存在するとき$Q$は上に有界であるという。
下界が存在するとき$Q$は下に有界であるという。
上界、下界が両方存在するときは単に有界であるという。

$Q$の上界の全体の集合に最小元$m$が存在するとき、$m$を$Q$の 最小上界(least upper bound) 、または 上限(supremum) という。
このとき、$m=\sup Q$と表す。

$Q$の下界の全体の集合に最大元$m$が存在するとき、$m$を$Q$の 最大下界(greatest lower bound) 、または 下限(infimum) という。
このとき、$m=\inf Q$と表す。

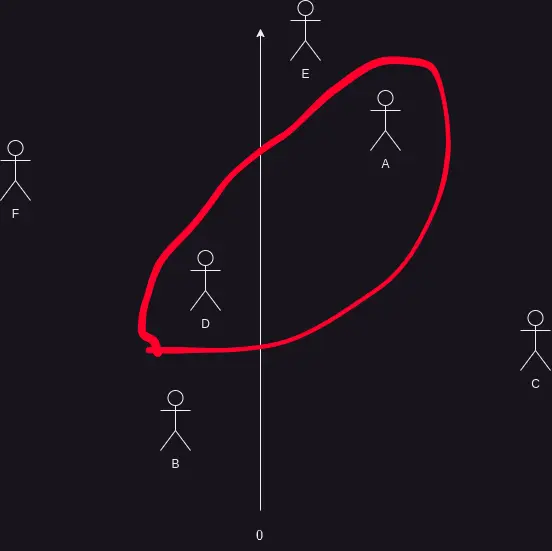
画像内の人間全体の集合を$P$として、赤線で囲まれた部分集合を$Q$とする。
順序は高さで与える。

つまり、例えば$A < E$である。

このとき、$Q$の上界は$A, \space E$の2つであり、下界は$D, \space C,\space B$の3つである。

そして、$\sup Q=A$であり、$\inf Q = D$である。

上界、下界の定義には$<$ではなくて$\leqq$が登場しているので間違えないように注意。

上界、下界の定義や上の具体例から分かるとおり、$\max Q, \space \min Q$(最大元、最小元)が存在すれば$\sup Q = \max Q, \space \inf Q = \min Q$である。

最大元、最小元は常に存在するとは限らないことに注意。

上界、下界が存在する場合でも上限、下限が存在するとは限らない。